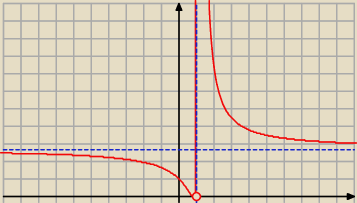
Asymptoty funkcji Julaa: Dana jest funkcja f(x) = e^x_x−1 (e do potęgi x/(x−1) Jakie ta funkcja ma asymptoty? pionowa x=1 ? pozioma y=e ?

Artur_z_miasta_Neptuna: tak i tak ... a pionowa jest jednostronna −−− pamiętaj o tym

Julaa: Tak, prawostronna.

Julaa: Brak punktów przecięcia z OX i OY?

Artur_z_miasta_Neptuna: yyyyy dlaczego o ile z osią OX się zgodzę (funkcja wykładnicza bez przesunięcia w pionie) o tyle z osią OY x=0 ... e⁰ = 1

Artur_z_miasta_Neptuna: przecież z osią OY zawsze będzie przecięcie jeżeli tylko x=0 należy do dziedziny

Julaa: ok, no tak. Brak miejsc zerowych pochodnej? i nie może mi wyjść kiedy f`(x)>0 a kiedy f`(x)<0

Artur_z_miasta_Neptuna: e^x/(x−1)

	x		x−1 − x
f' = ex/(x−1)* (		)' = ex/(x−1) *
	x−1		(x−1)2

tak ... brak miejsc zerowych zauważ, że: e^x/(x−1) >0 (wynika chociażby z braku miejsc zerowych + asymptoty pionowej) −1 <0 (x−1)² > 0 więc jakiego znaku będzie f'(x)

Julaa: no ujemna.

Julaa: czyli większa od zera należy do pustego, a mniejsza od zera w calej dziedzinie?

Artur_z_miasta_Neptuna: czyli f'(x) < 0 w D_f' czyli f↘ w (−∞,1) i w (1,+∞)

Julaa: Jeśli pochodna nie jest równa zero to nie może mieć ekstremum?

Artur_z_miasta_Neptuna: tak ... bo skoro ekstremum jest tylko wtedy gdy funkcja zmienia monotoniczność... a tutaj jest malejąca na przedziałach) (−∞,1) i (1,+∞)

Julaa:

	1
W punkcie (		, e−1) jest punkt przegięcia?
	2