Funkcja kwadratowa. Zadania luca5: 1. Wyznacz najmniejszą i największą wartość funkcji y=−2x² +4x+3 w przedziale <0,2> 2. Dana jest funkcja f(x)=−x²+3x−2 a) oblicz miejsca zerowe funkcji i podaj jej wzor w postaci iloczynowej b) dla jakich argumentów wartości funkcji f są ujemne? c) znajdź zbiór wartości funkcji f d) określ dla jakich argumentów funkcja f rośnie. 3. Rozwiąż: a) −3x+x²=0 b) −2x²−5x+3>0 4. Dla jakich argumentów wartości funkcji y=−x²−4x należą do przedziału (−∞,3> ? 5. Znajdź wzór funkcji kwadratowej, wiedząc, że funkcja ta przyjmuje wartości ujemne wyłącznie w przedziale (2,6) oraz że do wykresu należy punkt A=(3,−6) 6. Liczbę 16 przedstaw jako różnicę dwóch liczb tak, aby suma ich kwadratów była najmniejsza. Baardzo proszę o pomoc. Z matematyki jestem naprawdę zielona i nie wiem jak się za to zabrać Z góry bardzo dziękuje

Edyta PK: zad1 sprawdzamy czy wierzchołek funkcji należy do przedziału x_w=−b/2a x_w=−4/(2*(−2))=1 wierzchołek należy do przedziału podstawiasz do wzoru funkcji końce badanego przedziału i wierzchołek − obliczamy y f(0)=3 f(2)=3 f(1)=5 odp. W badanym przedziale funkcja osiąga wartość najmniejszą równą 3 i wartość największą równą 5.

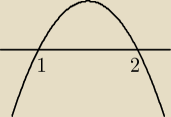
Edyta PK: zad2. a) obliczasz deltę i miejsca zerowe Δ=(−b)²−4ac=3²−4*(−1)*(−2)=1 x₁=(−b−√Δ)/2a=2 x₂=(−b+√Δ)/2a=1 postać iloczynowa y=a(x−x₁)(x−x₂) y=−(x−2)(x−1) b) a<0 wykres jest "smutny" wartości funkcji są ujemne dla x∊(−∞,1)∪(2,+∞) c)a<0 funkcja osiąga maksimum w y_w=−Δ/4a y_w=¹₄ ZW: y∊(−∞,¹₄) d) x_w=−b/2a=³₂ funkcja rośnie w przedziale x∊(−∞,³₂)

Edyta PK: zad.3 a) −3x+x²=0 x(−3+x)=0 x=0 lub x=3 b) −2x²−5x+3>0 Δ=49 x₁=¹₂ x₂=−3 odp. x∊(−3,¹₂)

Edyta PK: zad.4 y=−x²−4x a<0 funkcja "smutna" za y wstawiasz 3 −x²−4x=3 −x²−4x−3=0 Δ=4 x₁=4 x₂=−3 odp. Wartości funkcji należą do danego przedziału dla x∊(−∞,−3)

Edyta PK: zad.4 y=−x²−4x a<0 funkcja "smutna" za y wstawiasz 3 −x²−4x=3 −x²−4x−3=0 Δ=4 x₁=4 x₂=−3 odp. Wartości funkcji należą do danego przedziału dla x∊(−∞,−3)

Edyta PK: zad.5 ponieważ f−cja przyjmuje wartości ujemne na danym przedziale (2,6) to a>0 funkcja przechodzi też przez trzy punkty (3,−6) (2,0) (6,0) podstawiamy je do ogólnej postaci funkcji i otrzymujemy układ równań z trzema niewiadomymi, pamiętając, że a>0 −6=9a+3b+c 0=4a+2b+c 0=36a+6b+c wystarczy rozwiązać układ równań i otrzymujemy a=2 b=−16 c=24 y=2x²−16x+24

luca5: Dziękuje bardzo!

luca5: Dziękuje bardzo!

Edyta PK: zad.6 x pierwsza liczba x−16 druga liczba x−(x−16)=16 x²+(x−16)²=? x²+x²−32x+256=2x²−32x+256 y=2x²−32x+256 a>0 funkcja ma minimum w (x_w,y_w) 2x²−32x+256=0 x²−16x+128=0 Δ=−256 brak miejsc zerowych x_w=8 y_w=64 pierwsza liczba 8 druga liczba (8−16)=−8 8−(−8)=16 8²+(−8)²=64

mika: y=2(x−1)²−3 zw

PAWEŁ: 2X2−2X+5+2+2+4−X2

stefan: oblicz najmniejszą i największą wartość funkcji y=−2x²−4x=1 w przedzale <−2;2)

Saba: podaj trzy postacie funkcji kwadratowej i narysuj wykres y=−2x2+x+1

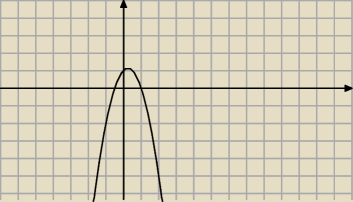
5-latek: 1−postac ogolna 2 postac kanoniczna 3 postac iloczynowa