parametr m
Lu: Dla jakich wartości parametru m dziedziną funkcji f jest zbiór liczb rzeczywistych?
a)f(x)=log(mx2−4x+m+3)
b)f(x)=log0,5 |mx2+2√2x+m+1|
Zacząłem robić przykład a
Na początku myślałem, że trzeba zrobić na dwa założenia że
a>0 i a=0
Δ<0 b=0
c>0
ale chyba jestem w błędzie bo w odpowiedzi (przykład a) jest m>1
Jak powinno się to zrobić? Proszę o pomoc.
9 sty 19:23
krystek: wylicz Δ i podaj kiedy <0 jak zapisałaś(−eś )
9 sty 19:27
h: a)
zalozenia
a>0
Δ<0
mx2−4x+m+3
m>0
Δ=(−4)2 − 4*m*(m+3)
Δ=16−4m2−12
Δ=−4m2+4
−4m2+4>0
−4(m2−1)>0
m2−1<0 żeby całość (−4(m2−1)) była większa
m2−1<0
m2<1
m ∊ (−∞;−1) suma (1;+∞)
sumując z drugim warunkiem
m ∊ (−∞;−1) suma (1;+∞) część wspólna m>0 = m>1
9 sty 19:28
jikA:
A jak byś chciała dostać b = 0? Dla jakiego m ∊ R dostaniesz taką sytuację?
9 sty 19:28
jikA:
Po za tym jeżeli a = 0 ∧ b = 0 ∧ c = 0 to otrzymujesz log0 a to nie należy do dziedziny.
9 sty 19:29
Lu: h, a tam nie powinno być 12m?
9 sty 19:30
Lu: policzyłem delte i delte(m) i wyszło mi m1=1 m2=4 ⇒ przedział (−∞,1)u(4,∞) a w przypadku f.
linowej c>0 ⇒ m>−3
9 sty 19:33
Lu: wiec jak to należy zrobic?
9 sty 19:34
Lu: pomoże ktoś?
9 sty 19:45
Lu: pomoże ktoś?
9 sty 19:46
Lu: pomoże ktoś?
9 sty 19:46
Lu: proooooooooszę

!
9 sty 19:51
Lu: 
9 sty 20:20
Lu: czy ktoś byłby może łaskaw pomóc mi z tym zadaniem?
9 sty 20:27
krystek: 19:28 masz rozwiązane.
9 sty 20:28
krystek: Przeczytaj uważnie polecenie

!
9 sty 20:28
Lu: tam jest zle wymnożone
Δ=(−4)2 − 4*m*(m+3)
Δ=16−4m2−12
powinno być 12m !
wiec to nie moze byc dobre rozwiazanie
9 sty 20:35
Lu: dzięki........
9 sty 20:42
polo: czemu a>0 ?
4 paź 19:11
polo: proszę o pomoc
4 paź 19:13
ZabardzoEhh: Bo cała funkcja ma być większa od 0 więc parabola musi mieć ramiona skierowane w górę wiec a>
0,funkcja nie mmoże mieć też miejsc zerowych więc Δ<0. Nie wiem tylko co ze sprawdzeniem, gdy
m=0. Wychodzi że x<3/4 ale co w związku z tym to nie wiem.

23 paź 10:34
ZabardzoEhh: Już wiem. Gdy m=0 to x <3/4 więc dziedziną funkcji nie jest zbiór liczb rzeczywistych
co znaczy, że zero musimy wyrzucić z naszych m−ów.

1 lis 09:27
kuba301: A jakie założenia trzeba dać do b)

?
12 lis 21:19
Miskqu: b)
jest wartosc bezwzgledna wiec nie musi byc a>0, (czyli m>0)
robisz poprostu tak: liczymy delte
Δ= −4m2−4m+8
musisz sprawic aby caly wykres byl pod albo nad osią x (masz wartosc bezwzgledna wiec moze byc
pod, i tak sie odbije)
liczysz Δm= 16*4*(−4)*8=144>0 −> mniejsza od zera bo nie ma przecinac osi x
√Δm= 12
m1= 1
m2=−2
wiec ostatecznie masz m∊(−∞,−2)∪(1,+∞)
25 sty 15:24
Miskqu:
w a) byl blad w delcie Δ=16−4m
2−12m
i dalej:
Δ<0 ( bo ma nie przecinac osi x)
Δm= 784
√Δm= 28
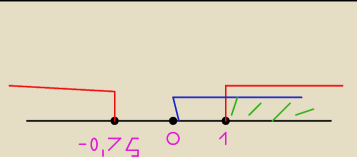
m1= −0,75
m2= 1
czyli m∊(−
∞,−0,75)∪(1,+
∞)
i dodadkowo warunek od ciebie że a>0 czyli m>0;
robimy część wspolną ( rysunek na gorze) i mamy m>1
25 sty 15:30
 !
!

 !
!


 ?
?
 w a) byl blad w delcie Δ=16−4m2−12m
i dalej:
Δ<0 ( bo ma nie przecinac osi x)
Δm= 784
√Δm= 28
m1= −0,75
m2= 1
czyli m∊(−∞,−0,75)∪(1,+∞)
i dodadkowo warunek od ciebie że a>0 czyli m>0;
robimy część wspolną ( rysunek na gorze) i mamy m>1
w a) byl blad w delcie Δ=16−4m2−12m
i dalej:
Δ<0 ( bo ma nie przecinac osi x)
Δm= 784
√Δm= 28
m1= −0,75
m2= 1
czyli m∊(−∞,−0,75)∪(1,+∞)
i dodadkowo warunek od ciebie że a>0 czyli m>0;
robimy część wspolną ( rysunek na gorze) i mamy m>1