monotonicznosć i ekstrema maniek: Jak mam zbadać monotoniczność i ekstreme funkcji f(x)= xlnx

jikA: Wyznaczasz dziedzinę następnie liczysz f'(x) ustalasz dziedzinę f'(x) sprawdzasz dla jakich x f'(x) > 0 f'(x) < 0 oraz f'(x) = 0 i liczysz ekstrema o ile są.

maniek:

	1		x
tylko ja nie wiem w jaki sposób, liczę pochodna f'(x)=( xlnx)' = x*		=		=1
	x		x

czyli wykresem funkcji jest prosta? czy źle liczę?

jikA: Źle liczysz masz musisz skorzystać z pochodnej iloczynu funkcji.

maniek: pochodną policzyłem według przykładu, który robiliśmy an wykładach

h: f(x)=x * lnx (x * lnx)' = (f * g)' = f'g + fg'

	1
(x * lnx)' = lnx + 1*
	x

	1
f'(x)=lnx+
	x

maniek: ok, teraz jak mam z tej pochodnej wyznaczyć monotoniczność, bo nie mam pojęcia

jikA: A wyznaczyłeś dziedzinę funkcji i dziedzinę pochodnej funkcji?

maniek: D:R D': R bez 0

jikA: Do poprawy. Poczytaj sobie co jest dziedziną funkcji logarytmicznej.

h: czemu D=R bez 0? przeciez nigdzie nie dzielisz przez 0 ani nic takiego musisz tylko spojrzec na logarytm naturalny log_b a b≠1 a>0 w tym wypadku b=e czyli jest ≠1 czyli tylko a> 0 czyli x>0 czyli D=(0;+∞)

jikA: h dobrze pisał bo ustalał dziedzinę pochodnej a tam dzieli przez x.

jikA: Dla logarytmu log_ba dziedziną jest 0 < b ≠ 1 ∧ a > 0 a nie tylko b ≠ 1.

maniek: przypuśćmy że rozumne, co mam dalej robić? Jestem z tego zielony bo nie mam z czego się uczyć,a w necie podobnego zadania nie znalazłem

jikA: Więc skoro ustaliliśmy że dla x ∊ (0 ; ∞) wyrażenie ma sens liczbowy to powiedz czy

1
	będzie > 0 czy może < 0 tak samo ln(x) będzie > 0 czy < 0 dla x ∊ (0 ; ∞).
x

maniek:

1
	>0
x

ln(x) >0

jikA: Sprowadź do wspólnego mianownika.

	1
ln(x) +		> 0
	x

xln(x) + 1
	> 0
x

I teraz badasz dla jakich x jest to większe.

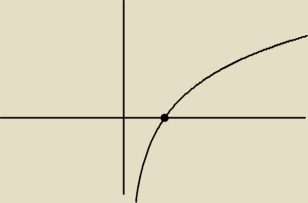
jikA: Niestety nie rozumiesz. Zobacz jak wygląda wykres funkcji y = ln(x) lub innej funkcji logarytmicznej o podstawie większej od 1.

maniek:

jikA: Czyli dla x ∊ (0 ; 1) funkcja y = ln(x) jest ujemna a Ty napisałeś że jest > 0.

maniek: teraz rozumne

jikA: Zastanawiałem co jest źle a to h źle policzył pochodną i uwierzyłem mu na słowo i nie sprawdziłem go. maniek policz jeszcze raz pochodną.

maniek: właśnie liczę pochodną, podstawiłem do wzoru, który podał h i mi wyszło lnx+1

jikA: I to jest poprawnie obliczone teraz liczysz kiedy ln(x) + 1 > 0.

maniek: no dla x>0 coś słabo dzisiaj kumam

jikA: Musisz policzyć dla jakich x wyrażenie ln(x) + 1 > 0.

maniek: na dzisiaj wystarczy, przez fizykę mam mętlik w głowie, jutro do tego wrócę

jikA: ln(x) > −1 ln(x) > −ln(e)

	1
ln(x) > ln(		)
	e

	1
x >
	e

	1
Dla x ∊ (		; ∞) funkcji f(x) jest rosnąca.
	e

Zostało Ci do policzenia f'(x) < 0 oraz f'(x) = 0 i zbadanie ekstremum. Masz duże zaległości z matematyki z liceum i powinieneś je jak najszybciej nadrobić bo będzie tylko coraz gorzej.

maniek: dzięki

jikA: Powodzenia.