Pomocy.. Olaaa:): x−1/x+1 + x+1/x−1>10/3

M:

ona:

x−1		x+1		10
	+		>
x+1		x−1		3

D: x+1≠0. x−1≠0 x≠−1 x≠1 D=R|{−1, 1}

(x−1)(x−1)		(x+1)(x+1)		10
	+		−		>0.
(x−1)(x+1)		(x−1)(x+1)		3

itd.

Jolanta:

x2−1+x2+2x+1		10
	−		>0
x2−1		3

(2x2+2x)*3−10(x2−1)
	>0
3(x2−1)

6x2+6x−10x2+10
	>0
6x2−3

−4x2+6x+10
	>0 /:2
6x2−4

−2x2+3x+5
	>0
3x2−2

Iloraz jest dodatni jeżeli licznik i mianownik są dodatnie lub jeżeli licznik i mianownik da ujemne 1) −2x²+3x+5>0. i 3x²−2>0 Δ=b²−4ac=9+40=49. (√3x−√2)(√3x+√2)>0.

	−b−√Δ		−3−7
x1=		=		=2,5. √3x−√2=0. √3x+√2=0
	2a		−4

	−b+√Δ		−3+7
x2=		=		=−1. x=√2/3 x=−√2/3
	2a		−4

Parabola ramiona w dół Parabola ma ramiona w gore −2x²+3x+5>0 dla x∊(−1; 2,5). i. 3x²−2>0. dla x∊(−∞,−√2/3) v(√2/3;∞) Część wspólna przedziałów x∊(−1 ;−√2/3)v(√2/3 ; 2,5) 2)−2x²+3x+5<0. i. 3x²−2<0 Rozwiązujemy Rozwiązaniem jest sumą przedzialow z 1) i 2)

ona:

x2−2x+1+x2+2x+1		10(x2−1)
	−		>0. /*3
x2−1		3(x2−1)

	2x2+2		10x2−10
3		−		>0
	x2−1		x2−1

6x2+6−10x2+10
	>0
x2−1

16−4x2
	>0
x2−1

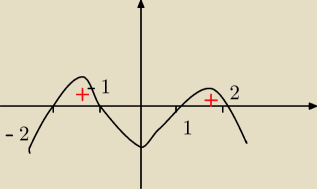
(16−4x²)(x²−1)>0 (4−2x)(4+2x)(x−1)(x+1)>0 x₁=2. x₂=−2 x₃=1. x₄=−1 a<0 oraz y>0 uwzględniając dziedzinę rozwiązaniem jest x∊(−2, −1)v(1, 2)