geometria analityczna Saizou : witam, wczoraj były wielomiany a dzisiaj niech będzie geometria analityczna

Ajtek: Cześć Saizou, czyżbyś się nudził wybitnie?

Saizou : Ajtek witaj, nie nudzę się tylko się przygotowuje do sprawdzianu

Saizou : up

Monza: LOL to kup sobie zbiorki maturalne

Saizou : wolę "żerować" na innych forumowiczach

asdf: nic nie zastąpi książki

Ajtek: Z analitycznej nie mam żadnego zbioru

Saizou : a może nauczyciel

denatlu: oblicz pole czesci koła ograniczonej prostą o równaniu y=√3x−2√3, obrazem tej prostej w symetrii względem osi OY i tą częscią okręgu x²+y²=12, która leży ponad osią OX

Saizou : czyli co mam obliczyć bo już zgłupiałem

Ajtek: To o co proszą w treści zadania

Uleńka: ja mam kilka zad z geometrii analitycznej 1) Dany jest okrąg o równaniu (x+4)² + (y−3)²=25. Do tego okręgu nie należy punkt ...? 2) Okrąg o równaniu x²+4x+y²−16y+20=0. Środek tego okręgu nie należy do prostej ... ? 3) dane jest okrąg o równaniu x²−6x+y²+14y+11=0. Środek okręgu nie należy do prostej ... ? 4) Wspólczynnik kierunkowy prostej o równaniu 2x−12y+11=0 jest równy ... ? 5) Odległość między punktami A=(2,−5) i B=(−7,1) jest równa ... ? 6) Środek okręgu o równaniu (x+6)²+(y−2)²=16 jest jednocześnie środkiem odcinka AB jeśli ... ? a to nie wszystkie

l: a może obliczyłbyś to? bardzo proszę Mały zakład produkuje dwa rodzaje stolików. Wyprodukowanie dużego stolika wymaga 3 godzin maszyny A i 1 godziny pracy maszyny B. Wyprodukowanie małego stolika wymaga 2 godzin pracy maszyny A i 1 godziny pracy maszyny B. W ciągu tygodnia maszyna A może pracować co najwyzej 120 godzin, a maszyna B − co najwyżej 50 godzin. Zakład zarabia na sprzedazy dużego stolika 175 zł, a na sprzedaży małego − 95 zł. Ile stolików dużych i małych powinien wyprodukować w ciągu tygodnia ten zakład aby, osiągnąć maksymalny zysk? Ile będzie wynosił ten zysk ?

Piotr: no jak co ? pole czesci kola

Saizou : hehehe czyli mam obliczyć fragment koła który jest ograniczony prostą i jej obrazem

denatlu: ja to czytałem wolno wolno wolno i nic. Potem szybko aby tylko przelecieć i jakiś wniosek już mi się nasunął . Chyba w tym zadaniu za dwa punkty powinno być pokonanie trudności odczytania polecenia . Odpocznij chwile i podejdź raz jeszcze. Ajtek jeśli ogarniasz prawdopodobieństwo, to byłbym wdzięczny za odpowiedź w moim temacie

Saizou : pole koła, które leży nad osią X i ograniczone jest obrazem prostej

Ajtek: Cześć Piotr . Jak ja dawno Ciebie nie widziałem na forum

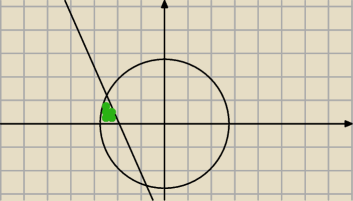
Saizou : czyli trzeba obliczyć zielony fragment

Ajtek: Coś rysunek mi się nie podoba...

Piotr: czesc Ajtek no w sumie nie jestem za duzo na forum. Saizou 2 proste i czesc kola nad osia OX.

Maslanek: Trochę tak Trójkąt powinien wyjść Później chyba najprościej wyznaczyć f(0). Punkt przecięcia f(x) z okręgiem. Wektor AB (gdzie A−f(0), B−punkt przecięcia)

	1
I P=		det[AB,−AB]?
	2

Maslanek: No nie... To jednak łatwiejsze jeszcze xD Miejsca zerowe funkcji i przeniesienie .

	1
Wtedy AB i P=		det[AB,−AB]
	2

FunkcjaPomocnaDłoń: Przepraszam, że sięwtrącam Panowie, ale mamy tu może jakiegoś mistrza z modułów?

Monza: Tak

FunkcjaPomocnaDłoń: |x+y| + |x−y| ≤6 Czy mógłbyś mi proszę podać potrzebne założenia do rozwiązania tego? Jakoś się w tym zagubiłem. Byłbym wdzięczny.

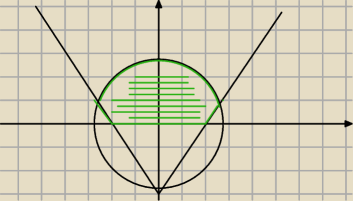
Saizou : to coś zielonego

Piotr: no chyba

Ajtek: Dlaczego odnoszę wrażenie, że bez całki tego się nie zrobi

Piotr: a co tam nawymyslal Maslanek

Ajtek: Radosna twórczość, tak jak pierwszy rysunek Saizou

Piotr:

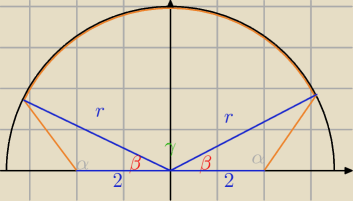
Saizou : r=2√3 α=120^o β=30^o

	2*2√3*sin30		1
Pt=		=2√3*sin30=2√3*		=√3
	2		2

2P_t=2√3 γ=180−60=120

	120		1
Pw=		*π*(2√3)2=		*4*3π=4π
	360		3

P_f=4π+2√3

Saizou : przepraszam że tak późno ale coś musiałem jeszcze zrobić

Saizou : to może jeszcze coś

Saizou :

Saizou : i tylko bez jednokładności poproszę

jikA: Dany jest okrąg o promieniu r i środku S (0 ; n). Jakie warunki spełniają współrzędne środka okręgu i długość promienia jeżeli okrąg ten ma z parabolą daną wzorem y = x² dokładnie dwa punkty wspólne?

Saizou : na pewno n>0 a co do r to jeszcze myślę

Maslanek: Nie spojrzałem na punkt przecięcia z OY Tak to by było jak mówiłem xD

Saizou : a co do r to brak pomysłów

jikA: Tworzysz układ równań.

⎧	x2 + (y − n)2 = r2
⎩	y = x2

Saizou : ja dzisiaj już nic nie wymyślę, życzę miłej nocy i spadam

Saizou : czyli o n dobrze myślałem

jikA: Dobranoc.