Koła K1 i K2 mają wspólny środek...
Siwy: Koła K1 i K2 mają wspólny środek. Promień K1 ma długość 10 cm, a pole K2 stanowi 1/4 pola K1.
Poprowadzono rónoległe styczne do K2. Oblicz pole figury, która jest ograniczona okręgiem K2,
poprowadzonymi stycznymi i okręgiem K1.
2 cze 19:54
kosma: Eee nie wiem, może ktoś mądrzejszy to zrobi?
2 cze 20:47
Bogdan:
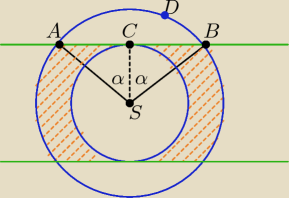
Wskazówki:
|SA| = |SB| = 10
|SC| = 5 (dlaczego?)
|AC| = |BC| =
√102 − 52 =
√75 = 5
√3
| | |SC| | | 5 | | 1 | |
cosα = |
| = |
| = |
| ⇒ α = 60o. |
| | |SB| | | 10 | | 2 | |
P
D − pole odcinka ABDA koła.
P
W − pole wycinka ASBDA koła
P
T − pole trójkąta ASB
P
P − pole pierścienia kołowego (K
1 − K
2)
P
F − pole szukanej figury.
P
D = P
W − P
T
P
F = P
P − 2P
D
2 cze 21:36
 Wskazówki:
|SA| = |SB| = 10
|SC| = 5 (dlaczego?)
|AC| = |BC| = √102 − 52 = √75 = 5√3
Wskazówki:
|SA| = |SB| = 10
|SC| = 5 (dlaczego?)
|AC| = |BC| = √102 − 52 = √75 = 5√3