granica funkcji asdfghjkl: lim_x→0(cosx)^1_x

asdfghjkl: lim_x→01+(cosx−1)^{1_cosx−1*cosx−1_x}=e⁰=1

asdf: a nie powinno być: lim_x→0 (cosx)^1/x2?

asdf: jak tak to: lim_x→0(1+cosx−1)^1/x2 = lim_x→0[(1+cosx−1)^1/cosx−1]^cosx−1/x2 = lim_x→0[(1+cosx−1)^1/cosx−1]^cosx−1/x2 = e.. do potęgi i teraz policzę:

	cosx−1		−(1−cosx)
limx→0		=limx→0		=
	x2		x2

	−(1−cosx)(1+cosx)		−sinx2
limx→0		= limx→0		=
	x2(1+cosx)		x2(cosx+1)

	−sinx*sinx		−1*1*1		−1
limx→0		=		=
	x*x(1+cosx)		1+1		2

więc całość:

	1
e−1/2 =
	√e

asdfghjkl: ale to chyba analogicznie się robi.NIe pomyliłam się

asdf: cosx−1/x = 0/0.

asdfghjkl: (cosx)^1_x=[1+(cosx−1)]^{1_cosx−1*cosx−1_x}=e⁰=1

asdfghjkl:

	1		1
i jeszcze mam pytanie do limx→0(		−[		])
	x		x

tutaj badamy prawostronne i lewo.

asdfghjkl:

jikA: Czy na pewno masz

1		1
	−		= 0?
x		x

asdfghjkl: nie rozumiem

jikA:

	1		1		1		1
Pytasz o granicę limx → 0 (		−		) a więc		−		= 0 tak więc
	x		x		x		x

lim_{x → 0} 0 = 0.

asdfghjkl:

	1		1
limx→0		−[		]
	x		x

to drugie to całość

asdfghjkl:

asdfghjkl:

	1		1
limx→0		−[		]
	x		x

jikA:

	1
A wiesz jak wygląda wykres [		].
	x

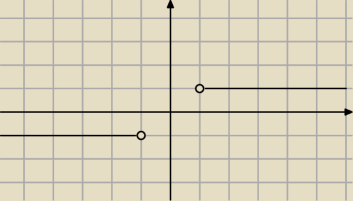
asdfghjkl: tak mi się wydaje że takwygląda

asdfghjkl:

asdfghjkl: [1/x]−1/x pomyliłam się w przepisywaniu

jikA:

	1
A co się dzieje w okolicy 0? Dla x = 2 mamy y = [		] = 0 więc wykres masz
	2

po prawej stronie źle i dlaczego po lewej stronie kropka jest nie zamalowana? Dla x = −1 mamy

	1
y = [		] = −1.
	−1

asdf:

	1
limx→0
	x

z lewej strony dąży do −∞; z prawej do ∞, wniosek?

asdfghjkl: to badamy teraz granie z praweji lewej strony tylko właśnie jak to zrobić

asdfghjkl: lim_x→0⁻−∞−∞=−∞ lim_x→0⁺+∞−∞=0

asdf: wyobraź sobie... lim_x→0⁻, czyli te wartości tak dążą do 0..dążą i dążą, ale nigdy nie "zdążą" . Te wartości są mniejsze od zera (granica lewostronna). np. x= −0.01

1		1
	=		= − 100
x		−0.01

dla x = −0.001 f(x) = −1000 i tak cooooraz blizej i coooraz blizej to granica = −∞ prawostronną samemu dasz rade.

jikA: A wiesz ile wynosi ∞ − ∞? Skąd?

Bobek: Bo to logiczne jak 1−1

Bobek: Tak samo ∞/∞=1

asdf: jakbys znał granicę ∞ (której nie znasz i chyba nikt nie zna) to byś mógł powiedzieć, że jest to 0.

Bobek: Bóg = ∞ Ma granice nieskończoną

asdfghjkl: czyli Hospitala uzyć w prawostronnej?

Bobek: de'Hospital

asdfghjkl: lim_x→0⁺(−x⁻²−x⁻²)=0

jikA: Bobek a wiesz że istnieje coś takiego jak wyrażenia nieoznaczone i właśnie ∞ − ∞ jest tym symbolem nie oznaczonym czy nie wiedziałeś?

Bobek: asdfghjkl −−> bzdura

Bobek: Oj, ludzie. Trochę poczucia humoru asdfghjkl−−> A podstaw sobie ułamki np.: 1/20000000, 1/222222222000000

asdf: @asdfghjkl

	1		1
Ja Ci zrobiłem rozwiązanie do		, a nie U{1}[x} −		...(tu nie widzę sensu)
	x		x

P.S Ale ostrożnie, może masz rację, bo alfą i omegą to ja na pewno nie jestem

asdfghjkl: dlaczego źle?

Bobek: Bo jaka to jest funkcja, którą podałeś/aś?

asdfghjkl:

1		1
	−[		]
x		x

Bobek: limx→0+(−x−2−x−2)=0 Pytam o to

Bobek: Bzdurę napisałem, zaraz poprawię

Bobek: limx→0+(−x⁽−2)−x⁽−2))=0 Granica ta nie jest równa 0.

asdfghjkl: lim_x→0⁺[∞−∞]=lim_x→0⁺(−x⁻²−x⁻²)= to iler wynosi

asdfghjkl:

asdfghjkl: pomoże mi ktoś?

asdfghjkl: halo/

asdf:

	1		1		2
−		−		= −		...
	x2		x2		x2

w lim x→0⁻ to masz −∞ (liczba do kwadratu da dodatnią, czyli masz na plusie)

a
	= ∞ (0 − granica)
[0]

tak samo dla x→ 0⁺ masz → −∞ więc granicą w punkcie x₀ = 0 masz −∞

asdfghjkl:

	1
a jeżeli bym miał limx→0x*[		]
	x

jikA:

	1
Pochodna z [		] ile wynosi?
	x

asdfghjkl: z lewej strony −∞ a z prawej ∞

jikA:

	1
A jak policzyłaś pochodną dla [		]?
	x

asdfghjkl: −x⁻²

asdfghjkl: a nie powinno się z lewej i prawej?

paula2: KTO POMOZE MI W ZADANKU? PROSZE

jikA: Poczytaj i zobacz jak się liczy granicę z cechy http://www.matematyka.pl/241632.htm

jikA: Nie granicę a pochodną źle napisałem.

asdfghjkl: wychodzi mi z lewej i prawej −∞

asdfghjkl:

asdfghjkl: prosze

asdfghjkl: halo?

asdfghjkl:

asdfghjkl:

asdfghjkl: jak to zrobić?

asdfghjkl: proszeee

asdfghjkl: ?

asdfghjkl: ←

asdfghjkl:

paula2: pomoze mi ktos w zadaniu