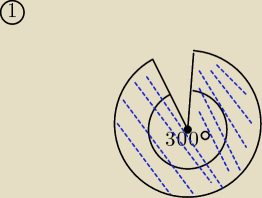
 Na rysunku przedstawiono wycinek koła o promieniu 10. Oblicz pole powierzchni całkowitej
stożka, ktorego powierzchnią boczną po rozcięciu jest ten wycinek.
Na rysunku przedstawiono wycinek koła o promieniu 10. Oblicz pole powierzchni całkowitej
stożka, ktorego powierzchnią boczną po rozcięciu jest ten wycinek.
| π*102*3000 | ||
Pb=Pwycinka koła | = | |
| 3600 |
| Pb | ||
r= | = | |
| πl |
| 300 | 5 | |||
Pbs=Pw= | πR2= | *π*102=.. | ||
| 360 | 6 |
| 300 | 5 | |||
ł= | *2 π*R= | *2π*10 | ||
| 360 | 6 |
| 5 | ||
2πr= | *2π*10⇔ | |
| 6 |
| 5 | ||
r= | *10 | |
| 6 |
| 50 | 25 | |||
r= | = | |||
| 6 | 3 |
| 25 | ||
Ppodstawy=πr2=π*( | )2 dokończ | |
| 3 |