Działania na wektorach Rosumad: Treść zadania: Uzasadnij, że długość odcinka łączącego środki ramion trójkąta jest równy połowie długości podstawy tego trójkąta. Mam to uzasadnić za pomocą wektorów, niestety, nie wiem jak... Nie chce rozwiązania zadania, tylko podpowiedź...

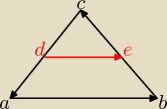
Rosumad: Jak wykazać, używając wektorów, że wektor DE jest równy połowie wektora AB?

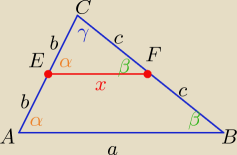
Eta: Z podobieństwa trójkątów ABC i EFC ..........

MQ: Wektorowo, to tak:

	1
CE→=		CB→
	2

	1
CD→=		CA→
	2

	1		1		1		1
DE→=CE→−CD→=		CB→−		CA→=		(CB→−CA→)=		AB→
	2		2		2		2

Rosumad: Dziekuje bardzo Eta i MQ.

pigor: ... lub z twojego Rosumad rysunku : de^→= da^→+ab^→+be^→ i de^→= dc^→+ce^→ ⇒ /+ stronami ⇒ 2de^→= (da^→+dc^→)+ab^→+(be^→ce^→) ⇔ 2de^→= 0^→+ab^→+0^→ ⇔ ⇔ 2de^→=ab^→ ⇔ de^→= ¹₂ab^→ , czyli wektory de^→ i ¹₂ab^→ są równe, a więc są równoległe i maja tę samą długość, tzn. de^→||ab^→ i de=¹₂ab c.n.u .