wielomiany Saizou : może jakieś zadanko z wielomianów tylko proszę nie zasypywać mnie nimi i nie aż takie "pomysłowe" (to do ICSP i ZKS)

asdf: Wykaż, że wielomian x⁴ − 2x³ + 2x² − 6x + 9 nie ma pierwiastków rzeczywistych.

Saizou : x⁴−2x³+x²+x²−6x+9=0 x²(x²−2x+1)+1(x²−6x+9)=0 x²(x−1)²+1(x−3)²=0 wielomian miałby miejsca zerowe gdy x=0 lub x=1 i x=3 a taka sytuacja nie istnieje cnu

jikA: To może coś takiego nie wiem czy kiedyś je widziałeś na forum. Wykaż że dla każdego a ∊ R spełniona jest nierówność a⁴ − a + 1 > 0.

Saizou : może jakaś podpowiedź

jikA: Podpowiedź: zastosuj myk trick 0 = m − m.

Saizou : a⁴+1>a + komentarz lewa strona jest zawsze dodatnia, nawet przy a→0,bo jest wtedy sumą liczby bardzo małej i 1, zatem jest większa od a→0. Dla ujemnych lewa strona jest zawsze większa od prawej, a dla a→+∞ lewa też jest zawsze większa od prawej czy tak może być

asdf: ktoś chyba się wolframem posłużył

Saizou : asdf jeśli chodzi o mnie to nie

jikA: Wolę inną odpowiedź taką ładną żeby było widać czarno na białym że to jest spełnione. Spróbuj zastosować podpowiedź m − m = 0 aby coś dodać i odjąć.

Saizou : brak pomysłów jedyne co mi przychodzi do głowy to a⁴−a²+a²−a−1>0

jikA: O właśnie o to chodzi teraz już z górki powinno być.

Saizou : a²(a²−1)+a²−a−1>0 niebieskie jest zawsze dodatnie i czerwone również

Mat: a²(a²−1)²>0

Saizou : czerwone jest zawsze nie ujemne

Saizou : Mat twój wielomian jest 6 stopnia

Mat: dobra jak już macie odpowiedź to

jikA:

	1		1		1
To kolejna podpowiedź 1 =		+		+		.
	4		4		2

Teraz już powinieneś zauważyć coś.

jikA: I tam pomyliłeś się nie −1 tylko 1.

ZK: zadanie . dla jakich wartosci parametrow a,b ic wielomian x³+5x²+6x+2 jest podzielnikiem wielomianu x⁴+8x³+ax²+bx+c Nastepne Dla jakich wartosci a i b trojmian x²+x+1 jest podzielnikiem wielomianu ax²0+bx¹9+1.

jikA: a⁴ − a² + a² − a + 1 > 0

Saizou : jestem ślepy albo czegoś nie widzę

jikA: Pomyśl chwilę na spokojnie nie potrzebie chcesz zrobić na szybko i może nie widzisz tego jeszcze.

Saizou : ZK 1) W(x)=x⁴+8x³+ax²+bx+c W(x)=(x³+5x²+6x+2)(kx+l)=kx⁴+(5x+l)x³+(6k+5l)x²+(2k+6l)x+2l k=1 5k+l=8→l=3 a=6*1+5*3=21 b=2*1+6*3=20 c=2

jikA: Dalej nie chce się poddać zdanie?

Maslanek: a⁴−a+1>0

	1		1		1
a4−a2+		+a2−a+		+		>0
	4		4		2

	1		1		1
Stąd (a2−		)2+(a−		)2+		>0
	2		2		2

Słowo komentarza...

jikA: Maslanek .

Maslanek: Jak się zna rozwiązanie (które podałeś), to żadna trudność Mozna by robić przez pochodne właściwie , powinno wyjść

Mat: To może coś takiego: wykaż że dla każdego xeC W(x)=x⁵−5x³+4x jest podzielny przez 120.

Saizou : taką jakąś zaćmę miałem

asdf:

	(a3−1)(a−1)
a4 +		> 0
	a+1

	(a3−1)(a−1)
a4 > −
	a+1

Saizou : x(x⁴−5x²+4)=x(x⁴−x²−4x²+4)=x[x²(x²−1)−4(x²−1)]=x(x²−1)(x²−4)=(x−2)(x−1)x(x+1)(x+2) jest to podzielne przez 5 chyba czegoś brakuje

asdf: jest podzielne przez 5 i jest podzielne przez 6

Saizou : a metoda komentarzowa może być

jikA: Jest to podzielne przez co najmniej 5! iloczyn pięciu kolejnych liczb.

Saizou : to i tak mamy podzielność przez 30 a nie przez 120

Mat: chyba może być; wychodzi iloczyn pięciu kolejnych liczb całkowitych więc... git

asdf: to jest 5 kolejnych, czyli 5! = 120

Mat: wśrod nich jest dokladnie jedna podzielna przez 5 , przynajmniej jedna przez 3 i 4 i do niej jeszcze jedna podzielna przez 2 .

Saizou : i znowu oczywistej rzeczy nie widziałem coś kiepski wieczór dzisiaj

Mat: w(x)= x⁵ + ax⁴ −bx³ −3bx² +2cx + 12 g(x)=x³ + 4x² + x −6 w(x) jest podzielny przez g(x) , znajdź a,b,c.

Saizou : W(x)=(x³+4x²+x−6)(ex²+fx+g) trzeba by to wymnożyć i przyrównać to co będzie stać przy x⁵ do 1 oraz wyraz wolny do 12 i obliczyć a,b,c,d

Mat: a co powiesz na g(1)=0 ?

Saizou : co więcej e = 1

Saizou : też można by rozłożyć wielomian G(x) do postaci iloczynowej i obliczyć układ W(x₁)=0, W(x₂)=0 W(x₃)=0

Mat: yhy

Saizou : W(−3)=0 W(−2)=0 W(1)=0 i trzeba by to obliczyć, ale to pozostawię na kiedyś indziej

jikA: Jeszcze chętny na jakieś zadanie czy starczy?

Saizou : możecie jeszcze coś wrzucić

Mat: Dobrze Ci idze ode mnie już ostatnie W(x)= x³ +px + q ma 3 rożne pierwiastki Udowodnij że p jest liczbą ujemną

Saizou : a,b,c pierwiastki wielomianu W(x)=(x−a)(x−b)(x−c)=x³+(b−a−c)x²+(ab+bc+ca)x−abc a z tego wniosek że wszystkie pierwiastki są dodatnie, albo 2 ujemne i jeden dodatni

Saizou : źle p ma być ujemne a nie q

Mat: niestety nieee....

Mat: btw i przed x² b jest również na misusie teraz coś z tym trzeba zrobić

Saizou : a może jakaś podpowiedź

Mat: przyrównaj to co wyszło do tej postaci z zadania, napisz czym jest p i q ... i czym x²

Saizou : −a−b−c=0 ab+bc+ca=p −abc=q i zapewne trzeba by to obliczyć

Mat: z pierwszego : a+b+c=0 (a+b+c)(a+b+c)=0 wymnażam a daje mi to 2(ab+ac+bc)<0 nawias to p , c.k.d. zmykam , dobranoc

jikA: Wyznacz wartości parametru m ∊ R dla których równanie (x² − 2x + m − 2)(|x − 1| − m + 1) = 0 ma trzy różne pierwiastki rzeczywiste. Oblicz te pierwiastki.

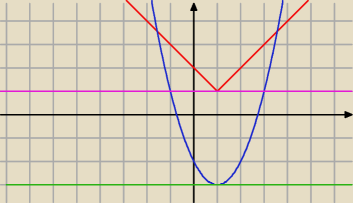
Saizou : x²−2x+m−2=0 lx−1l−m+1=0 x²−2x−2=m lx−1l+1=m wystarczy sprawdzić dla m=−3 lub m=1 dla m=−3 x²−2x−5=0 lub lx−1l+4=0 1 miejsce zerowe brak miejsc zerowych dla m=1 x²−2x −1=0 lub lx−1l=0 Δ=4+4>0 2 miejsca zerowe 1 miejsce zerowe zatem ten parametr to m=1 ale da 3 chyba też

Saizou : już wiem gdzie jest błąd, trzeba sprawdzić dla 3 a nie −3, bo wtedy funkcja kwadratowa ma 1 pierwiastek i by się zgadzało zatem m=1 i m=3

Saizou : ja już dzisiaj nie myślę całe od początku robię to zadanie

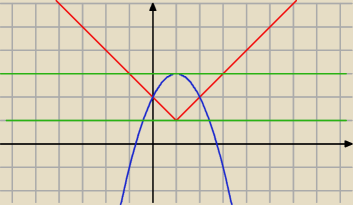
Saizou : x²−2x+m−2=0 lx−1l−m+1=0 −x²+2x+2=m lx−1l+1=m dla m=1 x²−2x−1=0 lx−1l=0 Δ>0 1 pierwiastek 2 pierwiastki dla m=3 x²−2x+1=0 lx−1l−2=0 (x−1)²=0 2 pierwiastki 1 pierwiastek zatem m=1 lub m=3 i jest to ostatnie zadanko na dzisiaj

jikA: Dobrze dla m = 1 ∨ m = 3 tylko jeszcze pierwiastki wystarczy obliczyć i wszystko w porządku.

Saizou : dla m=1 x₁=1−√2 x₂=1+√2 x₃=1 dla m=3 x₁=1 x₂=−1 x₃=3

Saizou : to ja lecę narazie

jikA: Dobranoc.