Geometria analityczna ALE-ZADANIE: Mam zadanie o takiej treści: Napisz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka C w trójkącie ABC, gdzie A(−1,2) B(7,6) C(1,7). Chciałbym, żebyście sprawdzili mój tok myślenia, ewentualnie korygując błędy. W tym zadaniu zacząłbym od schematycznego rysunku. Następnie obliczę długość podstawy, czyli odcinka |AB|. Po tym, postaram się uzyskać równanie prostej dzięki wzorowi (x2−x1)(y−y1)=(y2−y1)(x−x1). Po tym jak uzyskam prostą w formie y=ax+b, zmienię znak przy współczynniku kierunkowym a oraz "odwrócę" liczbę. Uzyskam w ten sposób prostą zawierającą wysokość poprowadzoną z wierzchołka C? Pozdrawiam

yepa: wydaje mi się, że dobrze myślisz, ale napisze dla pewności: 1. znalezienie rownania prostej przechodzacej przez punkty AB, a wlasciwie interesuje nas tylko wspolczynnik kierunkowy 'a' 2. znalezienie prostej prostopadlej do prostej z pkt. 1 przechodzacej przez punkt C; czyli dla prostej z punktu 1 postaci: y = ax + b i C(1,7) wygladaloby to tak: y = −(1/a)x + b 7 = −(1/a)*1 + b itd.

Artur_z_miasta_Neptuna: wszystko ładnie pieknie ... czyli dobrze ... ale po co Ci długość odcinka |AB| jest to w tym zadaniu całkowicie zbyteczne

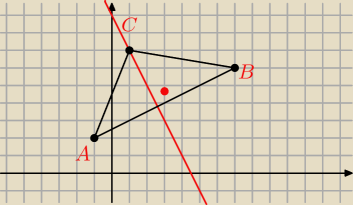
Aga1.: Zrobiłabym krócej obliczając współczynnik kierunkowy prostej AB.

	4		1
a=		=
	8		2

Prosta CD jest prostopadła do AB, przechodzi przez punkt C, jej współczynnik kierunkowy wynosi −2 y=−2x+b 7=−2+b, b=9 Szukana prosta y=−2x+9.

ALE-ZADANIE: No właśnie też nie wiem po co chciałem liczyć odcinek |AB|, jakieś przyzwyczajenie bo ostatnio rozwiązuję masę podobnych zadań Dziękuję wszystkim za odpowiedzi, ostateczny wynik też wychodzi mi y=−2x+9.

pigor: ... lub wektorowo np. tak : niech D=(x,y) − spodek wysokości, to AB^→⊥ CD^→ ⇔ [8,4] * [x−1,y−7]=0 ⇔ 8(x−1)+4(y−1)=0 ⇔ ⇔ 2x−2+y−7=0 ⇔ 2x+y−9=0 − szukane równanie wysokości w postaci ogólnej .

ALE-ZADANIE: Łooo, tej metody nie znam, mam matematykę w LO na poziomie podstawowym

ALE-ZADANIE: Ale dziękuję, douczę się w ferie