potrzebuję ekstrema i punkt przegięcia Sebcio: Potrzebuję pomocy. Przebieg zmienności funkcji: g(x)=x*lnx

Damian: dla ekstemow liczysz pochodna 1 a dla pkt przegiecia 2 pochodna dziedzina to x(niesk,0)u(0,niesk)

Damian: wrooooc dziedzina (0,niesk) pomylilem sie

Sebcio: ok, dzięki

Damian: ale liczac pp to funkcja U bedie na przedziale (0,niesk) i nie bedzie osiagac p przegiecia

Sebcio: dobra, dobrze, ze mowisz, bo kurde do konca nie wiem co robie

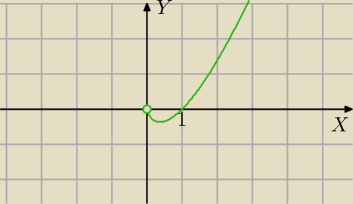
Mila: 1)D=(0;∞) 2) miejsca zerowe f(x) x*lnx=0 i x∊D lnx=0⇔x=1

	lnx
2) lim {x→0+}(xlnx)=lim		H=0
	1   x

lim {x→∞}(xlnx)=∞

	1
3) f '(x)=1*lnx +x*		=lnx +1
	x

4) Ekstrema i monotoniczność f(x)

	1
lnx+1=0⇔lnx=−1⇔x=e−1=
	e

	1		1
lnx+1>0⇔lnx>−1⇔lnx>ln(		)⇔x>		funkcja rosnąca
	e		e

	1		1		1		1		1
dla x=		jest minimum f(		)=		*ln		=−
	e		e		e		e		e

	1
5) f '' (x)=(lnx+1) ' =
	x

1
	≠0 dla x∊D brak punktów przegięcia
x

6) sprawdź asymptoty ukośne licz dalej

Sebcio: Mila, jesteś moim wybawcą i bohaterem

Mila: Miło, że się przydało.