Geometria przestrzenna Monza: Trudne Punkty A,B,C i D leżą na sferze o promieniu długości 3. OBlicz długość odcinka AD wiedząc że AD = BD = CD oraz kąty ASB = CSA = BSC = 90 stopni

Artur_z_miasta_Neptuna: hmmm ... zapewne S ma oznaczać środek tejże sfery ... tak

Monza: Niedobrze przepisałem. Powinno być tak: ADB = CDA = BDC

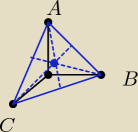
Artur_z_miasta_Neptuna: niech S będzie umiejscowiony w początku układu współrzednych (0_xyz), punkty A,B,C będą znajdować się odpowiedni na osi OX,OY,OZ w dodatnich częściach tychże osi Punkt D' będzie równo odlegly o każdego z tych trzech punktów, jeżeli będzie on środkiem ciężkości trojkata równobocznego tworzonego przez te punkty. mając współrzędne punktu D' jestes w stanie wyznaczyć współrzędne punktu D ... który leży na prostej przechodzącej przez punkt S oraz D' ... oraz odcinek |SD| = 3 (uwaga ... dwa możliwe położenia punktu D)

Artur_z_miasta_Neptuna: ejjj ... to mi całe zadanie rozwaliłeś ... wstydziłbyś się

Artur_z_miasta_Neptuna: na pewno ADB = CDA = BDC = 90^o bo to mi źle pachnie

Artur_z_miasta_Neptuna: jest to niemożliwe czegoś takiego nie da się skonstruować (aby D było na sferze)

Monza: 26 str 71 Poziom R Matematyka krok po kroku zbiorek No to nie wiem Spytam się mojej pani od matematyki która jest autorka ksiażki na maila

Artur_z_miasta_Neptuna: oczywiście można zaznaczyć te trzy punkty ... jak wrócę z psiakiem to siądę do tego zadania ... jak sobie w myslach umiejscowi te punkty to dalszy ciąg zadania to 'pikuś' i sprowadza się do zauważenia jednej rzeczy i użycia tw. pitagorasa

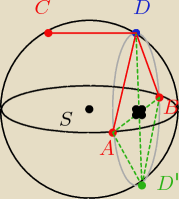
Artur_z_miasta_Neptuna: Krok 1 ... obieramy sobie punkt D na sferze (dowolne polożenie) Krok 2 ... kulę przecinamy płaszczyzną (jak na rysunku) i aby kąt ADB = 90^o to punkty A i B muszą leżeć w taki wlasnie sposób (wynika to z tw. o kątach opartych na tym samym łuku oraz założeniu zadania o równych odleglościach |AD| = |BD| Krok 3 ... zaznaczymy punkt D' (na rysunku) Krok 4 ... punkt C wyznaczamy z wektora normalnego płaszczyzny wyznaczonej w kroku 2 (innymi słowy ... odcinek CD ma być prostopadły do tej płaszczyzny ... dzięki czemu CDE = 90^o gdzie punkt E to dowolny punkt (poza D oczywiście) należący do tej płaszczyzny ... w szczególności punkt A i B ... ale także punkt D') Krok 5 ... sferę przecinamy płaszczyzną zawierającą punkty D,C,D' (rysunek w następnym poście) i zauważamy, że ta płaszczyzna zawiera środek sfery

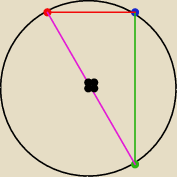
Artur_z_miasta_Neptuna: Krok 6 ... z kroku 4 wiemy , że trójkąt C,D,D' jest trójkątem prostokątnym Krok 7 ... z tw pitagorasa: (2*3)² = x² + (√2x)² ⇔ 36 = 3x² ⇔ x = 2√3 koniec zadania