Nierówność wielomianowa Mysza: Rozwiąż nierówność |x³−3x−2|≤x³−3x−2

Mysza: proszę pomóżcie

Aga1.: Szukaj ,na forum jest rozwiązana.

Artur_z_miasta_Neptuna: wystarczy trochę pomyśleć kiedy zachodzi taka nierówność: |a| ≤ a

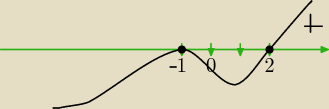
Mila: 1) |x³−3x−2|≤x³−3x−2 2) |x³−3x−2|=x³−3x−2 dla x³−3x−2 ≥0 w(x)=x³−3x−2 ; w(−1)=−1+3−2=0 wielomian dzieli sie przez (x+1) dzielę: x=−1 1 0 −3 −2 1 −1 −2 0 x³−3x−2 =(x+1)(x²−x−2) (x²−x−2)=0 ; Δ=1+8=9

	1−3
x1=		=−1 lub x2=2
	2

(x+1)(x²−x−2)=(x+1)(x+1)(x−2)=(x+1)²*(x−2) (x+1)²*(x−2)≥0 ⇔x=−1 lub x≥2 ad1) dla x=1 lub x≥2 mamy nierówność: x³−3x−2≤x³−3x−2⇔0≤0 ⇔tam gdzie zachodzi równość , czyli x=−1 lub x≥2 ad 2 )dla x∊(−∞−1) ∪(−1;2) −x³+3x+2≤x³−3x−2⇔−2x³+6x+4≤0 /:(−2)⇔x³−3x−2≥0 w podanych przedziałach funkcja jest ujemna x∊Φ odp. x=1 lub x≥2

pigor: ... lub np. tak : ponieważ x³−3x−2= x³+1−3x−3= (x+1)(x²−x+1)−3(x+1)= (x+1)(x²−x−2)= (x+1)²(x−2), to |x³−3x−2|≤ x³−3x−2 ⇔ |(x+1)²(x−2)|≤ (x+1)²(x−2) ⇔ ⇔ (x+1)²|x−2|−(x+1)²(x−2)≤ 0 ⇔ (x+1)²(|x−2|₍x−2))≤ 0 ⇔ ⇔ x+1=0 lub |x−2|−(x−2)≤ 0 ⇔ x=−1 lub |x−2|≤ x−2 ⇔ ⇔ x=−1 lub x−2 ≥0 ⇔ x=−1 lub x ≥2 ⇔ x∊{−1}U<2+∞)