wklęsłość wypukłości i pkt przegięcia funkcji x/lnx. pomocy!
Izka222: proszę o obliczenie wklęsłości i wypukłości oraz punkty przegięcia funkcji x/lnx. to dla mnie
baaaardzo ważne i potrzebne na poniedziałek

pomóżcie

5 sty 19:36
Artur_z_miasta_Neptuna:
skoro jest to dla Ciebie bardzo ważne to dlaczego sama nie potrafisz tego policzyć

musisz policzyć y''
przyrównać do zera
naszkicować wykres y'' i na jej podstawie wyznaczyć punkty przegięcia oraz przedziały
wklęsłości i wypuklości funkcji (analogicznie do y' i monotoniczności)
5 sty 19:40
Artur_z_miasta_Neptuna:
a więc ... w czym problem

5 sty 19:40
Izka222: no właśnie nie potrafię

wszystko obliczyłam pochodna drugiego stopnia wyszła mi 2−lnx/ln
3x
z czego po przyrównaniu do zera wychodzi x = e
2 i problem jest z rysowaniem wykresu.
dziedziena wynosi df x∊(0,1)∪(1,+
∞) .
wg mnie funkcja na wykresie powinna przechodzić jedynie przez e
2 która jest pkt przegięcia a
wszędzie gdzie znalazłam tą funkcję przechodziła ona jeszcze przez 1. tylko nie wiem
dlaczego..
5 sty 19:50
Izka222: to jak, wytłumaczyłbyś mi jeśli możesz dlaczego przez tą 1 ta funkcja też przechodzi?
5 sty 19:58
Artur_z_miasta_Neptuna:
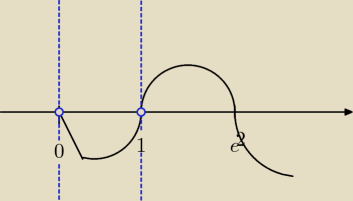
| 2−lnx | |
| = 0 ⇔ (2−lnx)*x*ln3x = 0 <−−− trzy punkty podejrzane o bycie miejscami |
| xln3x | |
zerowymi rysujesz
to że miejsce zerowe nie należy do dziedziny nie znaczy że funkcja nie zmieni tam znaku
przyklad:
| | 1 | |
f(x) = |
| ... nie ma miejsca zerowego w 0 ... a przecież na lewo od x=0 funkcja przyjmuje |
| | x | |
wartości ujemne a na prawo od x=0 wartości dodatnie

5 sty 20:03
Aga1.:
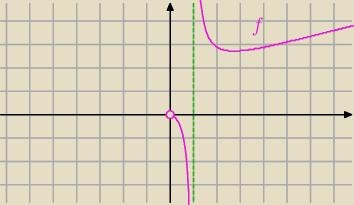
5 sty 20:06
Izka222: | | 2−lnx | |
ale dlaczego są trzy pkt skoro mam ten ułamek |
| = 0 potem mianownik usuwam i |
| | xln3x | |
zostaje mi się tylko 2−lnx = 0
−lnx=−2
lnx=2
x=e
2 i tylko to mi wyszło a tamte dwa pkty skąd?
5 sty 20:08
Artur_z_miasta_Neptuna:
a czy wiesz że mianownik jest zawsze dodatni

to czemu go usuwasz w takim razie

przy szukaniu miejsc punktow przegięcia nie popelnisz błędu ... ale później przy szkicu wykresu
już błąd popełniasz
zauważ, że dla x∊(0,1) licznik będzie dodatni ... ale mianownik juz nie

czyli cale wyrażenie
jest ujemne ... a według Ciebie jest dodatnie
5 sty 20:12
Izka222: aha.. to jak mam wyprowadzić z tego ułamka że x=0 ∪ x=1 ∪ x = e2 mógłbyś mi to rozpisać jakoś
?
5 sty 20:16
Izka222: zawsze na zajęciach mianownik usuwaliśmy mnożąc go przez 0 i to wszystko, nie wiedziałam że w
ten sposób trzeba
5 sty 20:18
Artur_z_miasta_Neptuna:
| 2−lnx | |
| = 0 //* (xln 3x) 2 <−−− mnożysz przez liczbę dodatnią  |
| xln3x | |
5 sty 20:18
Artur_z_miasta_Neptuna:
gdy mianownik jest dodatni np. x2ln4x <−−− taki byłby dodatni i byś się nim nie musiała
przejmować
5 sty 20:19
Artur_z_miasta_Neptuna:
tak naprawdę powinno się licząc monotoniczność czy też wypukłość
liczyć najpierw przyrownując do 0 (i byś zlikwidowala mianownik tak jak chciałaś)
a później osobno ... nierówność

i tu już nie mogłabyś tego zrobić tak jak chciałaś
jednak w praktyce robi się tylko równość i tu pojawiają się czasami problemy (patrz ten
właśnie przykład)
5 sty 20:21
Izka222: no tak rozumiem masz rację, nie pomyslałam o tym bo robiłąm to z przyzywczajenia że mnoży się i
już, tylko niestety nie wiem jak to rozpisać żeby to jakoś sensownie wygladało

5 sty 20:23
Artur_z_miasta_Neptuna:
tak jak napisałem ... mnożysz przez kwadrat
wypisujesz trzy miejsca zerowe ... z czego dwa nie należą do dziedziny (zaznaczasz że nie
należą do Df '' i robisz szkic
5 sty 20:24
Izka222: czyli dla upewnienia czy dobrze to napiszę sprawdź jeśli możesz

| 2−lnx | |
| = 0 / (xlnx3x) 2 |
| xln3x | |
iii potem 2−lnx=0
uwzględnie że muszą być trzy pierwiastki i potem
x = e
2 i tak po prostu dopisać że tamte to x=0 i x = 1 bo ..

?
po prostu chce to dobrze zrozumieć raz a porządnie

5 sty 20:31
Izka222: no bo nie mogę tak sobie napisać x = 1 i x=0 muszę dać jakieś uzasadnienei skąd sobie to
wzięłam
5 sty 20:33
Artur_z_miasta_Neptuna:
| 2−lnx | |
| = 0 / *(xlnx3x)2 |
| xln3x | |
(2−lnx)*x*ln
3x = 0
2−lnx = 0 ⇔ x = e
2
x = 0 ... x∉D
f ''
ln
3x = 0 ⇔ x = 1 ... x∉D
f ''
5 sty 20:33
Izka222: ahaaa coś takiego.. dziękuję Ci bardzo


i tam w tym ostatnim
e
ln3x=e
0
i potem od razu x=1 ?
nie robiłam tego po prostu ze zrozumieniem, bo teraz to ma sens

5 sty 20:41
Artur_z_miasta_Neptuna:
ln3x = 0 ⇔ lnx = 0 ⇔ x=1 koniec ... żadnego eln ...
5 sty 20:45
Izka222: ale jak jesli e jest do potęgi ln to one się tak jakby "kasują" , czy tam znoszą przynajmniej
tak się uczyłam? i poza tym 1 bo ===> e0 to 1
5 sty 20:47
Artur_z_miasta_Neptuna:
ale po co to

to jest niepotrzebne
nikt się Ciebie nie będzie pytał skąd wiesz że lnx=0 ⇔ x=1
tak samo jak nie będzie się pytał skąd wiesz że cosx=1 ⇔ x = 2kπ
przyjmuje że to wiesz i tyle
5 sty 20:49
Izka222: ok,ok ale to że jest tak jak napisałam to prawda no nie? jest tak że te e i ln się znoszą (to
już dla mojej własnej takiej pewności)
5 sty 20:52
Artur_z_miasta_Neptuna:
tak ... własności logarytmow alogab = b
5 sty 21:01
Izka222: ok dziękuję bardzo raz jeszcze za pomoc bardzo!

5 sty 21:03
 pomóżcie
pomóżcie 
 musisz policzyć y''
przyrównać do zera
naszkicować wykres y'' i na jej podstawie wyznaczyć punkty przegięcia oraz przedziały
wklęsłości i wypuklości funkcji (analogicznie do y' i monotoniczności)
musisz policzyć y''
przyrównać do zera
naszkicować wykres y'' i na jej podstawie wyznaczyć punkty przegięcia oraz przedziały
wklęsłości i wypuklości funkcji (analogicznie do y' i monotoniczności)

 wszystko obliczyłam pochodna drugiego stopnia wyszła mi 2−lnx/ln3x
z czego po przyrównaniu do zera wychodzi x = e2 i problem jest z rysowaniem wykresu.
dziedziena wynosi df x∊(0,1)∪(1,+∞) .
wg mnie funkcja na wykresie powinna przechodzić jedynie przez e2 która jest pkt przegięcia a
wszędzie gdzie znalazłam tą funkcję przechodziła ona jeszcze przez 1. tylko nie wiem
dlaczego..
wszystko obliczyłam pochodna drugiego stopnia wyszła mi 2−lnx/ln3x
z czego po przyrównaniu do zera wychodzi x = e2 i problem jest z rysowaniem wykresu.
dziedziena wynosi df x∊(0,1)∪(1,+∞) .
wg mnie funkcja na wykresie powinna przechodzić jedynie przez e2 która jest pkt przegięcia a
wszędzie gdzie znalazłam tą funkcję przechodziła ona jeszcze przez 1. tylko nie wiem
dlaczego..



 to czemu go usuwasz w takim razie
to czemu go usuwasz w takim razie przy szukaniu miejsc punktow przegięcia nie popelnisz błędu ... ale później przy szkicu wykresu
już błąd popełniasz
zauważ, że dla x∊(0,1) licznik będzie dodatni ... ale mianownik juz nie
przy szukaniu miejsc punktow przegięcia nie popelnisz błędu ... ale później przy szkicu wykresu
już błąd popełniasz
zauważ, że dla x∊(0,1) licznik będzie dodatni ... ale mianownik juz nie  czyli cale wyrażenie
jest ujemne ... a według Ciebie jest dodatnie
czyli cale wyrażenie
jest ujemne ... a według Ciebie jest dodatnie

 i tu już nie mogłabyś tego zrobić tak jak chciałaś
jednak w praktyce robi się tylko równość i tu pojawiają się czasami problemy (patrz ten
właśnie przykład)
i tu już nie mogłabyś tego zrobić tak jak chciałaś
jednak w praktyce robi się tylko równość i tu pojawiają się czasami problemy (patrz ten
właśnie przykład)


 ?
po prostu chce to dobrze zrozumieć raz a porządnie
?
po prostu chce to dobrze zrozumieć raz a porządnie 

 i tam w tym ostatnim
eln3x=e0
i potem od razu x=1 ?
nie robiłam tego po prostu ze zrozumieniem, bo teraz to ma sens
i tam w tym ostatnim
eln3x=e0
i potem od razu x=1 ?
nie robiłam tego po prostu ze zrozumieniem, bo teraz to ma sens 
 to jest niepotrzebne
nikt się Ciebie nie będzie pytał skąd wiesz że lnx=0 ⇔ x=1
tak samo jak nie będzie się pytał skąd wiesz że cosx=1 ⇔ x = 2kπ
przyjmuje że to wiesz i tyle
to jest niepotrzebne
nikt się Ciebie nie będzie pytał skąd wiesz że lnx=0 ⇔ x=1
tak samo jak nie będzie się pytał skąd wiesz że cosx=1 ⇔ x = 2kπ
przyjmuje że to wiesz i tyle
