ostroslupy edytaa43: Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny podstawy pod katem 30 stopni, a jej wysokość jest równa 3 √3.Oblicz objętość tego ostrosłupa.

edytaa43:

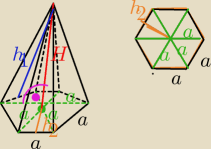
Mati_gg9225535: α − kat miedzy h₁ a h₂ V = ?

	1
h1 = 3√3 V =		Pp * H
	3

	1
α=30o V =		* 6 * PΔ * H
	3

	1		a2√3
sin30o =		V = 2 *		* H
	2		4

	√3		a2√3
cos30o =		V =		* H
	2		2

	a√3
h2 =
	2

	a2√3
PΔ =
	4

Mati_gg9225535:

	H
sin 30o =
	h1

	H
cos30o =
	h2

Mati_gg9225535: oj pośpiech

	h2
cos30o =
	h1

edytaa43: ale to byloby tak z sinusem 1 − rowna sie 3 √3 / h1 2 co potem wyszlo ze h1 wynosi 6 √3

Mati_gg9225535: h₁ masz podane w zadaniu

Mati_gg9225535:

1		3√3
	=		⇒ H= ?
2		H

edytaa43: w zdaniu jest podany H calej bryly

Mati_gg9225535: tresc zadania ktora podalas brzmi : "a jej wysokość jest równa 3 √3." wiec sprawdz jak jest w zadaniu jesli "jej" to jest wysokosc sciany bocznej, jesli "jego" to zgodze sie ze ostroslupa

edytaa43: sorry moj blad ,,jej

edytaa43: h2 wyniesie 4,5

edytaa43: dobrze?

Mati_gg9225535: tak

edytaa43: to do wzoru na pole tr rownobocznego musze wlasnie te 4,5 do kwadratu podniesc?

Mati_gg9225535:

	a√3
h2 to wysokosc a we wzorze masz a, dlatego podalem Ci wzor na H2 =		stad wylicz a
	2

Mati_gg9225535: mialo byc male h₂ =...

edytaa43: wyszlo 13,5 √3

Mati_gg9225535: ale co wyszlo Ci tak?

edytaa43: h² = a √3 / 2 (4,5)² = a √3/2 20,25 = a √3/2 /*2 40,5= a √3 a= 13,5 √3

Mati_gg9225535: h₂ nie h²

edytaa43: no tak to dobrze czy nie ?

Mati_gg9225535: no zle bo podnioslas do kwadratu a to nie ma byc h² tylko h₂ czyli

	a√3
4,5 =		/ *2
	2

9 = a√3

	9
a=
	√3

a= 3√3