Proszę się nie wcinać GrzesioCzesio: więc co do a) masz ustalić dziedzinę funkcji, czyli wszystkie wartości jakimi może być x i będzie to prawdziwe f(x)=√x²+1 wyrażenie x²+1 jest pod pierwiastkiem, a z tego co wiesz wyrażenie pod pierwiastkiem musi być zawsze większe albo równe 0 (x²+1≥0), więc jeśli nie widzisz od razu tego, że x² ZAWSZE jest większe albo równe 0 (x²=0 jeżeli x=0), że tamto pod pierwiastkiem zawsze będzie większe od 0, to liczysz z Δ. wsp. a przed x² jest dodatni (a=1), więc ramiona szłyby do góry, a delta wyjdzie ujemna, więc nie będzie wartości minusowych ( sprzecznych z założeniem o pierwiastku).

GrzesioCzesio: więc dziedzina funkcji to wszystkie liczby rzeczywiste, czyli Df=R

GrzesioCzesio: b) G(x)=x³−3x²+18 nie ma żadnych założeń dla których funkcja będzie nieprawdziwa ( pierwiastki, dzielenie itp.), więc od razu jako Df zapisuję R

GrzesioCzesio: c)

	x3−2
y=
	x2−9

	1
założenie tutaj to to, że nie wolno dzielić przez 0 np.		− niemożliwe, czyli trzeba
	0

znaleźć ( jeśli istnieją) takie x, dla którego x²−9=0 i wyrzucić je z dziedziny, więc x²−9=0 (x−3)(x+3)=0 x=3, x=−3 Df=R−{−3, 3}

GrzesioCzesio: pamiętaj: to co w liczniku jest ( czyli na górze) nie wpływa na dziedzinę, ofc jeśli nie ma tam jakichś pierwiastków albo cos tym stylu

GrzesioCzesio: d)

	√x+1
r(x)=
	x−1

nie jest funkcją wymierną ( tutaj nie mam pojęcia dlaczego jak coś, więc nic nawet nie rozpatruję

GrzesioCzesio: 4.7 sprawdź czy funkcje są równe

	x2−1
a) w(x)=		, f(x)=x−1
	x+1

na początku sprawdzasz dziedzinę pierwszej i drugiej funkcji dla w(x) jest to ( nie wolno dzielić przez 0, x+1=0, x=−1,) Df=R−{−1}, dla f(x)=x−1 jest to Df=R, więc nawet jeśli wyjdzie na końcu, że funkcje mają takie same wzory, to nie będą równe, bo nie mają takiej samej dziedziny, ale liczenie wzoru. Sprawdzasz czy są równe, więc układasz w(x)=f(x) i podstawiasz i sprawdzasz czy wyjdzie to samo.

x2−1
	=x−1
x+1

(x−1)(x+1)
	=x−1
x+1

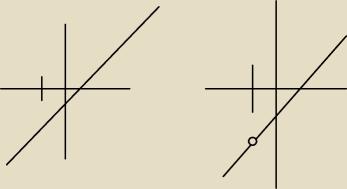
x−1=x−1 funkcje mają taki sam wzór, y=x−1, z tym, że jedna funkcja ma dziedzinę R, a druga R−{−1}, więc na rysunku jednej funkcji jest cały czas linia ciągła, a na rysunku drugiej w miejscu gdzie jest x=−1 trzeba zostawić niezamalowane kółko, coś takiego jak an rysunkach, więc odp brzmi: funkcje nie są równe.

tim: Mogę wiedzieć o co chodzi?

GrzesioCzesio: Resztę robi się tak samo

	−3x2−3
b) w(x)=		, f(x)=−3
	x2+1

Df W(x) x²+1=0, sprzeczność: zawsze będzie dodatnie, więc Df=R Df f(x)= R ( funkcja stała y=−3) dziedziny takie same, teraz wzory

−3x2−3
	=−3
x2+1

−3(x2+1)
	=−3
x2+1

−3
	=−3
1

−3=−3, funkcja ma taki sam wzór y=−3, ma taką samą dziedzinę, więc są równe, rysunek l

GrzesioCzesio:

	−2x4+2
c) w(x)=		, f(x)=−2x2−2
	x2−1

dziedzina w(x)

−2x4+2
x2−1

x²−1=0 (x−1)(x+1)=0 x=1, x=−1 Df=R−{−1,1} Df F(x), Df=R sprawdzanie równości

−2x4+2
	=−2x2−2
x2−1

−2(x4−1)
	=−2x2−2
(x−1)(x+1)

−2(x2+1)(x2−1)
	=−2x2−2
(x−1)(x+1)

−2(x2+1)(x−1)(x+1)
	=−2x2−2
(x−1)(x+1)

−2(x2+1)
	=−2x2−2
1

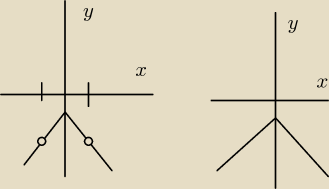
−2x²−2=−2x²−2 taki sam wzór, różne dziedziny więc wyglądają tak samo, ale trzeba na jednej uwzględznić niezamalowane kółka dla x=−1 i x=1 wygląd funkcji: miejsca zerowe −2x²−2=0 −2(x²+1)=0 x²+1=0, sprzeczność, zawsze większe od zera, Δ<0, więc nie zetknei się ani nie przetnie z osią OX na funkcji więc, wygląda mniej więcej tak:

GrzesioCzesio: d omine

tim: Dobrze się czujesz? O.o

GrzesioCzesio: 4.8, skróć ułamki

	4x3
a)
	16x2

ogólna zasada taka, ze skracasz podobne z podobnym ( liczby z liczbami, x z x, y z y itp.)

4x3		4x		1x		x
	=		=		=
16x2		16		4		4

podajesz założenie: x≠0, bo jeśli pod x podstawiłbym 0, to na samym początku w mianowniku na dole byłoby 0, a przez 0 nie można dzielić

	3x12		x12		x4
b)		=		=
	6x8		3x8		3

dalej tak samo

GrzesioCzesio: Tim, pierwsza sprawa: prosiłem się o nie wcinanie, a skoro używam zwrotów bezpośrednich, to logiczne jest że do kogoś konkretnego jest to pisane, więc...

GrzesioCzesio: ... tak, czuję się bardzo dobrze, nie licząc kataru i gardła

GrzesioCzesio: 4.9, skracanie ułamków cały myk polega na tym, żebyś zauważał że coś możesz wyciągać przed nawias itepe

	x2−4		(x−2)(x+2)		x−2
a)		=		=
	3x+6		3(x+2)		3

x≠−2 df=R−{−1}

	4x2−9		(2x−3)(2x+3)		(2x−3)(2x+3)		2x+3
b)		=		=		=		=−2x−3
	3−2x		−2x+3		−1(2x−3)		−1

−2x+3=0 2x=3

	3
x=
	2

	3
df=r−{		}
	2

reszta z wykorzystaniem różnych wzorów skrc mnożenia itp. na tej samej zasadzie

GrzesioCzesio: 4.10 to samo, tylko że bardziej skomplikowane liczenie

GrzesioCzesio: 4.11, też

GrzesioCzesio: 4.12 coś takiego

	3x		puste pole
a)		=
	4		16x

masz podać wartość dla "puste pole" ( tak sobie nazwałem) żeby było to równe, więc mnożysz na krzyż 3x*16x=4*puste pole 48x²=4*puste pole /:4 12x²=puste pole, więc w puste pole wstawiasz 12x²

	9x2		puste pole
b)		=
	27		81

9x²*81=27*puste pole 729x²=27*puste pole /:27 27x²=puste pole wstawiasz tak samo dalsza część zadania polega na tym samym

GrzesioCzesio: 4.13, to samo, tylko że masz obliczyć mianownik a nie licznik

GrzesioCzesio: dalej już mi się nie chce, idę się uczyć na poprawkę z chemii i dla kolo z PO, Nara i do jutra