. asdf: logarytm log_1/2 |logx − 2| ≤ 0 D: logx − 2> 0 → logx > 2 → x > 100 x > 0 log_1/2 |logx − 2| ≤log_1/21 |logx −2 | ≥ 1 dla x≥0 dla x < 0 logx − 2 ≥ 1 oraz logx − 2 ≤ −1 logx ≥ 3 oraz logx ≤ 1 x≥ 1000 oraz x ≤ 10 x∊<1000;∞) oraz x∊(−∞;0) uwzgledniajac dziedzine x∊<1000;∞) dobrze?

asdf: kurde, zle mam dziedzine logx − 2 ≠ 0 x≠ 100 oraz x > 0 ale odpowiedzi cos nie moge zrobić

Aga1.: Dz: x>0 i Ilogx−2I>0⇒logx≠2⇒x≠100 D=(0,100)U(100,∞) Ilogx−2I≥1 logx−2≥1 v logx−2≤−1 logx≥3 v logx≤1 x≥10³ v x≤10 Mi odp. wychodzi inna, sprawdź jeszcze.

asdf: log_1/2 | log(x) − 2 | ≤ 0 log(x) − 2 ≠ 0 x ≠ 100 i jeszcze tą najbardziej wewnętrzną dziedzinę: x > 0 D: x∊(0;100)(100;∞) log_1/2 | log(x) − 2 | ≤ log_1/21 | log(x) − 2 | ≥ 1 dla x ≥ 0 dla x < 0 log(x) − 2 ≥ 1 oraz log(x) − 2 ≤ −1 (x) ≥ 1000 oraz x ≤ 10 uwzgledniajac przedziały: x∊<1000;∞) oraz x∊(−∞;0) teraz uwzgledniając dziedzinę: x∊ <1000;∞) dobrze?

asdf: wolfram: http://www.wolframalpha.com/input/?i=log%5B1%2F2%2C+%7C+log%5B10%2C+x%5D+-+2%7C+%5D+%3C%3D+0 i dlaczego są tu x < 0 skoro jest log(x)... troche dziwne

Paweł: Aga1 moglabys spojrzec na moja pochodna?

Aga1.: Rozwiązałam Ci , podaj tylko odp. Zapis dla x<0 log(x)−2≤−1 nie ma sensu,bo nie istnieją logarytmy z liczb ujemnych, przecież dziedzinę na samym początku określiłeś

asdf: nom, określiłem, ale czy jest ona dobrze?, bo takie coś: |log(x) − 2| ≠ 0 to już tego "wewnętrznego" log(x) nie liczę bo on jest w wartości bezwzględnej tak?

asdf: jeszcze raz policzę dziedzinę: log_1/2 (| log(x) − 2)|) |log(x) − 2| <<pierw to log(x) − 2 ≠ 0 x≠ 100 a teraz ten wewnętrzny: x≠0? Df: x∊(−∞;0)(0;100)(100;∞)

Aga1.: log_ab=c⇔(b>0 i a>0 i a≠1 i a^c=b) liczba logarytmowna b zawsze większa od zera.

asdf: no tak, tylko dlaczego wolfram dał to: http://www.wolframalpha.com/input/?i=log%5B1%2F2%2C+%7C+log%5B10%2C+x%5D+-+2%7C+%5D+%3C%3D+0

Aga1.: Zastanawiam się , może później jeszcze spojrzę na to , bo w tej chwili nie widzę błędu w swoim rozwiązaniu.

asdf: A jaka wychodzi Ci odpowiedź?

Aga1.: Zaznaczyłam na osi liczbowe, dziedzinę i rozwiązanie

asdf: ale jedno mnie dziwi (pewnie zle rozwiazuje): dla x ≥ 0 log(x) − 2 ≥ 1 log(x) − 2 ≤ −1 tutaj trzeba dać przedzialy, ze dla pierwszego (dla x ≥0, dla drugiej nie rownosci: x < 0)

Aga1.: To co zapisałeś o 15:39 jest niepoprawne.

Aga1.: A jak rozwiążesz taką nierówność? Ix+1I>2 x+1>2 lub x+1<−2 tak?

asdf: to po prostu bez przedziałów?

asdf: nom, tak bym rozwiązał, tylko pierwsze dla x ≥0, drugie dla x < 0 tak?

Aga1.: Nie,rozwiązujesz nie przejmując się dziedziną, a dziedzinę uwzględniasz na samym końcu przy podaniu ostatecznej odpowiedzi.

asdf: to nie trzeba dawać przedziałów ?

Aga1.: Na pewno nie tych x≥0 i x<0 .

pigor: no to np. tak: log_¹2 |logx−2|≤ 0 ⇔ |logx−2| ≥ (¹₂)⁰ i (*) x >0 i |logx−2| >0 ⇒ ⇒ |logx−2| ≥ 1 i logx−2≠0 ⇔ (logx−2≤−1 lub logx−2 ≥1) i logx≠2 ⇔ ⇔ (logx≤ 1 lub logx ≥3) i x≠10² ⇔ (x≤ 10¹ lub x ≥10³) i x≠100 ⇒ stąd i z (*) ⇔ 0< x≤10 lub x ≥1000 ⇔ x∊(0; 10>U<1000;+∞) . ...

asdf: a jak mam takie coś:

	x+1
log1/3 |		| ≤ 0
	x

D: x∊ R / {−1;0}

	x+1
log1/3 |		| ≤ log1/31
	x

	x+1
|		| ≥ 1
	x

x+1		x+1
	≥ 1 oraz		≤ −1
x		x

x+1 ≥ x² oraz x+1 ≤ −x² −x² +x + 1 ≥ 0 oraz x² + x + 1 ≤ 0 Δ =√5 Δ<0 I co w takim czymś zrobić?

Aga1.: Licz x₁, x₂ , parabola, i rozwiązania nierówności , zamiast oraz jest lub więc tworzysz sumę rozwiązań nierówności , a na końcu wyznaczasz część wspólną z dziedziną i masz odp.

pigor: ... np. tak : w zbiorze D_n= R\ {0,−1} mamy kolejno |^x+1_x| ≥ 1 ⇔ ^|x+1|_|x| ≥ 1 / *|x| ⇔ |x+1| ≥ |x| /² ⇔ x²+2x+1 ≥ x² ⇔ ⇔ 2x+1 ≥ 0 ⇒ x ≥ −¹₂ i x≠0 ⇔ x∊<−¹₂;0)U(0;+∞) . ...

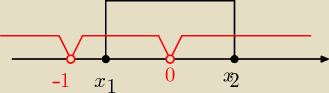
asdf: −x² + x + 1 ≥ 0 Δ = 5 √Δ = √5

	−1 +√5		1−√5
x1 =		=
	−2		2

	−1−√5		1+√5
x2 =		=
	−2		2

	1−√5		1+√5
x ∊ <		;		>
	2		2

x² + x + 1 ≤ 0 x∊∅ uwzględniając dziedzinę (x∊R/{−1;0}

	1−√5		1+√5
x∊<		;0)(0;		>
	2		2

tak?

asdf: źle...zaraz poprawię.

asdf:

x+1
	≥ 1 // x2
x

x(x+1) ≥ x² x² + x ≥ x² x ≥ 0

x+1
	≤ −1 // x2
x

x(x+1)≤−x² x² + x ≤ − x² 2x² + x ≤ 0 x(2x+1)≤0

	1
x≤0 u x ≥−
	2

D: x∊R /{0;−1} ODP:

	1
x∊<−		;0)(0;∞)
	2

tak?

Aga1.: Żle rozwiązałeś.

x+1
	≥1
x

x+1
	−1≥0
x

x+1−x
	≥0 /*x2
x

x≥0

Aga1.: i x≠0 to x>0 −−−jest to odp. do pierwszej nierówności.

asdf: później to uwzględniłem z dziedziną.