równania stycznych k1s2: Znajdź równania stycznych do okręgu x²+y²=1 przechodzących przez punkt P=(0,−5)

Artur_z_miasta_Neptuna: UWAGA styczna tworzy kąt prosty z promieniem okręgu 1) wylicz odległość punktu P od środka okręgu S 2) odległość ta to będzie przeciwprostokątna trókąta PSA ; gdzie A to punkt styczności 3) długość odcinka AS = r = 1 4) z tw. pitagorasa obliczasz długość odcinka PA 5) mając długość odcinka PA oraz współrzedne punktu P ... obliczasz współrzędne punktu A (będą dwie możliwości ) 6) wyznaczasz równanie prostej przechodzącej przez punkt P oraz A (osobno dla dwoch przypadków punktu A) koniec zadania

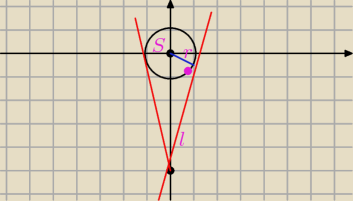Aga1.: Środek okręgu S(0,0), promień okręgu r=1 styczna przechodzi przez punkt (0,−5), więc jej równanie ma postać y=ax−5, a w postaci ogólnej l: ax−y−5=0 Odległość punktu S od prostej l jest równa promieniowi d=d(S,l)=r

	IAx0+By0+CI
d=
	√A2+B2

rozwiąż równanie i wylicz a.

I0+0−5I
	=1
a2+1

a²+1=5