Pilnie potrzebna pomoc Palulu: Prosta o równaniu x=3 jest osią symetrii wykresu funkcji kwadratowej f(x) =ax² +bx +14. Prosta o równaniu y= −4 ma z tym wykresem dokładnie jeden punkt wspólny. Dla jakich argumentów wartości funkcji f są dodatnie?

Artur_z_miasta_Neptuna: 1) skoro x=3 jest osią symetrii ... to znaczy, że dla x=3 ów funkcja przyjmuje wartość maksymalną/minimalną (x_wierzcholka) 2) skoro y=−4 (prosta równoległa do osi OX) posiada dokładnie 1 punkt wspólny z parabolą, to znaczy, że to jest wartość funkcji w wierzchołku (y_wierzchołka) masz wzory na x_w i y_w ... tworzysz układ równań i rozwiązujesz

Palulu: Dziękuję za cheć a można jeszcze bardziej to wytłumaczyć ?

Aga1.: Równanie osi symetrii x=p

	−b
Skoro x=3, to p=3 ⇒		=3⇒b=−6a
	2a

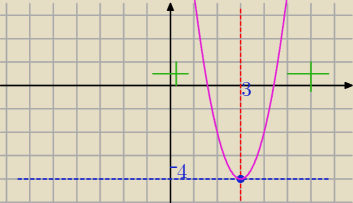
Prosta y=−4 przechodzi przez wierzchołek q=−4 Z tego wynika ,że wierzchołek znajduje się w punkcie W=(3,−4)⇒f(3)=−4 9a+3b+14=−4 b=−6a Oblicz a i b A następnie miejsca zerowe.