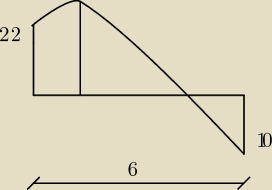
help beniu: Mam wykresy z mechaniki, może ktoś mi pomoże, w pewnym przedziale M(x) wynosi:

	52
M(x)=2x2−		x+10
	3

Chodzi mi o wyznaczenie ekstremum

zenon: Wystarczy policzyć pochodną: M'(x) = 4x + ⁵²₃. W miejscu, gdzie pochodna się zeruje (dla funkcji kwadratowej tylko w jednym) będzie ekstremum: 4x + ⁵²₃ = 0 4x = ⁵²₃ x = ⁵²₁₂ = ¹³₃<− w tym miejscu masz ekstremum. Jeżeli x wypadnie poza przedziałem M(x) sprawdzasz wartości M(x) na granicach przedziału. W p.p. podstawiasz w początkowym wzorze ¹³₃ w miejsce x i masz wartość ekstremum: M(¹³₃) = 4*(¹³₃)² + ⁵²₃*{13}{3} + 10. Jest jeszcze metoda obliczania wierzchołka paraboli z liceum, ale jej nie pamiętam. Zaletą liczenia pochodnej jest to, że działa dla wszystkich funkcji (tylko trzeba dodatkowo sprawdzić czy w granicach prawostronnych i lewostronnych pierwiastka pochodnej pochodna ma różne znaki).

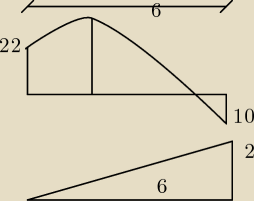
beniu: A może ktoś wie jak to scałkować z trójkątem ?

beniu: ekstremum 27,555

zenon: Co to znaczy "scałkować z trójkątem"?

beniu: nie wiem jak to nazwać "całkowanie graficzne" w budownictwie

Artur_z_miasta_Neptuna: pamiętaj ... moment przyjmuje wartość maksymalną gdy siła tnąca wynosi 0 też nie mam bladego pojęcia co się kryje pod pojęciem 'scalkować z trójkątem' podaj całe zadanie