pomocy
Lizzie: oblicz pole figury ograniczonej krzywymi o podanym równaniu.
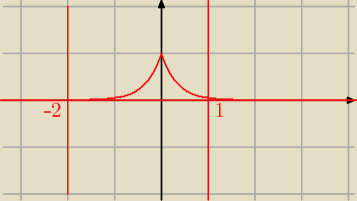
y=e−3|x| , y=0 , x= −2 , x= 1
4 sty 17:24
Godzio:
∫
−20e
3xdx + ∫
01e
−3xdx
4 sty 17:26
Lizzie: a jaki wynik ci wyszedl?
4 sty 17:38
Lizzie: bo mi 2+e−3+ e−3 dobrze?
4 sty 17:39
Godzio:
Raczej nie, popraw (jak się podstawi −2 to już wychodzi 3e−6 (
4 sty 17:40
4 sty 17:40
Lizzie: to jaki bedzie koncowy wynik?
4 sty 17:42
Godzio:
Najpierw podaj wyniki całkowania.
4 sty 17:43
Lizzie: | | 1 | |
będzie 1 + |
| e−6 + e−3 + 1 |
| | 3 | |
4 sty 17:53
Godzio: | | 1 | | 1 | | 1 | |
∫e3xdx = |
| e3x, na przedziale mamy: |
| − |
| e−6 |
| | 3 | | 3 | | 3 | |
Więc dalej źle
4 sty 18:03
Lizzie: | | 1 | |
ale jak wychodzi ci |
| − .... |
| | 3 | |
4 sty 18:07
Godzio:
A jak się liczy całkę oznaczoną
?
4 sty 18:11
Lizzie: no na granicach:
4 sty 18:17
Lizzie: za x podstawiamy obie granice
4 sty 18:18