matematykaszkolna.pl
. shm: Ściana boczna ostrosłupa prawidłowego trójątnego jest nachylona do płaszczyzny podstawy pod
 3 
kątem α, że sinα=
. Promień okręgu wpisanego w podstawę jest równy 2√3. Wyznacz pole
 5 
całkowite ostrosłupa.
4 sty 16:44
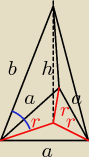
123_123_123_123: rysunekR = 2√3
 h 
sin α =
 b 
3 h 
=
5 b 
Dalej z proporcji a pozniej z tw. pitagorasa
4 sty 16:51
shm: A wyszła Ci odpowiedź 126√3 ? Bo ja nie wiem co źle robie.
4 sty 17:35
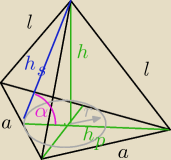
dero2005: rysunekr = 2√3 = 13hp ⇒ hp = 6√3
h 
= sinα = 35 ⇒h = 35hs
hs 
hs = √r2+h2
 5 
hs =
√3
 2 
a = 23√3hp = 5
 a2√3 
Pp =
= 254√3
 4 
 3 
Pb =
a*hs = 754√3
 2 
Pc = Pp + Pb = 254√3 + 754√3 = 25√3 przelicz działania
4 sty 22:02
harris:
 a√3 
a tu nie będzie hp=6√3 ⇒
=6√3 ⇒ a√3=12√3 ⇔ a=12 ?
 2 
4 sty 23:53
dero2005: rzeczywiście nastąpiła omyłka w liczeniu wg obydwu wzorów a = 12 Pp = 36√3, Pb = 45√3, Pc = 81√3
5 sty 21:54