Kofunkcje. O co w tym chodzi? Infor: Witam. Mam duży problem. Jutro mam kolokwium a nie rozumiem jednej rzeczy podobno prostej. Mógłby mi ją ktoś wytłumaczyć od A do Z i co z tego się bierze? Mam taki przykład 4[cos 10π−4/3π)+isin(10π−4/3π)]= 4(cos4/3π−isin4/3π)=4[cos(π+π/3)−isin(π+π/3)]=4(−cos π/3+isin π/3)=4(−1/2+√3/2i)=−2+2 √3 i Kolega mówił mi, ze chodzi tutaj o wzory redukcyjne. Nie rozumiem o co w tym chodzi. Dlaczego nagle zamieniają się znaki na przeciwne, dlaczego 10π−4/3π=4/3π i w ogóle. Mógłby mi ktoś w tym pomóc?

Artur_z_miasta_Neptuna: https://matematykaszkolna.pl/strona/430.html trzymaj 'studencie'

Infor: Znalazłem to już wcześniej, ale nie wiem jak je zastosować...

Infor: Pomożecie?

asdf: Proszę! 4(cos (10π − 4/3π) + isin(10π−4/3π) = Zauważ, że funkcja sin i cos jest okresowa, to znaczy, ze oscyluje, czyli sie powtarza co

	π		π
pewien przedział, jest nim 2π, więc czy to będzie wartość 2π+		, czy		to jest to
	2		2

samo (zobacz sobie na wykresie). Dlatego jezeli jest 10π to skracasz, jak było by 3π to wtedy masz: π+2π = π. Narysuj sobie koło i zobaczysz (π=180^o). 4(cos(−4/3π) + isin(−4/3π)) = tutaj korzystasz z tego, że cos(−x) = +cosx oraz sin(−x) = −sinx, więc aby sie pozbyc tych ujemnych kątów musisz właśnie z tego skorzystać 4(cos(+4/3π) − isin(4/3π)) = no i już masz..

	π		π
4(cos(π+		) − isin(π+		) =
	3		3

4/3π = π+π/3, czyli jest to 3 ćwiartka, dla sinusa i cosinusa są to znaki ujemne, patrz tutaj: http://www.matematyka.pl/latexrender/pictures/5/0/502802e591aa0eb7f6b6d65023def1a7.png 4( − cosπ/3 − (−sin(π/3)) = Zobacz ze kąty zostały sprowadzone do pierwszej ćwiartki, pozostało to odpowiednio uprościć: −(−) = + (tego chyba nie trzeba tłumaczyć) 4(−cos(π/3) + sin(π/3)) −4cosπ/3 + 4isinπ/3 odczytujesz z tabelki ile to jest π/3 i masz wynik.

asdf: Zapis: 4(cos(+4/3π) − isin(4/3π)) = no i już masz.. powinien wyglądać tak: 4(+cos(4/3π) − isin(4/3π)) = no i już masz..

Infor: Dlaczego 4(cos(π+π/3)− isin(π+π/3)= 4(−cosπ/3 − ( −sin(π/3))=? Gdzie podziało nam się te pierwsze π?

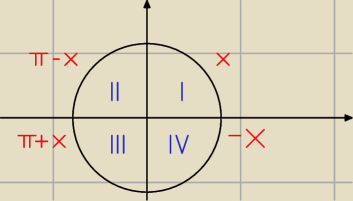
asdf: redukujesz do pierwszej ćwiartki, a później z tego korzystasz.

Infor: Redukuję do pierwszej ćwiartki? Nie rozumiem przepraszam. Już 7 godzina siedzenia przy matmie wyłączam się...

Infor: Resztę zrozumiałem tylko nie wiem dlaczego znika te jedno całe π...

asdf: to może zacznij od prostych zadań:

	12π		5π		5π
cos (		) = π +		= −cos
	7		7		7

	15π		π		π		π		π
cos(		) = cos(7π +		)= cos(π+2*3π +		) = cos(π+		) = − cos
	2		2		2		2		2

	47π		5π		5π
cos(		) =cos( 6π +		) = cos(		)
	7		7		7

Infor: Dalej nie rozumiem dlaczego np w pierwszym znika nam π...

asdf: ..musisz zredukować kąt do kąta ostrego (0;90) a pozniej korzystasz z tych zależności: https://matematykaszkolna.pl/strona/430.html Nie miales wyjasnionych tych wzorów na lekcjach czy nie uważałes? (jak to drugie to zajrzyj do natatek − pierwsze lekcje)

Infor: My lecimy z zadaniami od razu bez rozpisywania czasami i nie wiem później co się z czego bierze, stąd problemy. Tym bardziej jak miało się matematykę 6 lat temu... Już to zrozumiałem. Jeśli będę miał problemy będziesz jeszcze tutaj? Chciałbym pisać tutaj z problemami. Dziękuję bardzo za pomoc!

asdf: Pisz, na pewno ktoś Ci pomoze, ja za 2 godziny wracam, jak będę potrafił to Ci pomoge.

Infor: Dziękuję jeszcze raz!