matematykaszkolna.pl
Trygonometria Kostka: Kąt α jest ostry i tg α=2. Oblicz wartość wyrażenia 2cos2 α − 1
4 sty 12:29
Kostka: Dziękuję za zainteresowanie
4 sty 12:51
asdf: to ma być wartość podana, np. 2cos2x − 1 = 4? (to nie jest prawdziwy wynik).
4 sty 13:01
asdf:
sinx 
= 2
cosx 
sinx = 2cosx sin2x = 4cos2x
sin2x 
= 2cos2x
2 
sin2x 
−1 = 2cos2x − 1
2 
sin2x − 2 
= 2cos2x −1
2 
4 sty 13:09
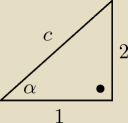
Patryk: rysunek1+4=c2 c=√5
 1 
cosα=
 √5 
2cos2α−1=
 1 
=2*(
)2−1=
 √5 
 2 
=
−1=
 5 
 2 5 
=
−
=
 5 5 
 3 
=−
 5 
4 sty 13:15
asdf: ..źle zrozumiałem treść: tgx = 2 sinx = 2cosx sin2x = 4cos2x sin2x + cos2x = 1 4cos2x + cos2x = 1
 1 
cos2x =
 5 
 2 3 
2cos2x − 1 =
− U{5]{5} = −
 5 5 
4 sty 13:26