. asdf: Treść: Nie używając postaci kanonicznej oraz równań na pierwiastki funkcji kwadratowej oblicz te wartości. mając równanie: 2x² − x − 2 chcę wyliczyć miejsce zerowe, bez wykorzystania równań na x₁ oraz x₂. Próbowałem to zrobić z kątem prostym, ale czegoś mi brakuje Liczę normalnie deltę: Δ = 1 + 2*2*4 = 17

	−Δ		−17		1
q =				= −2
	4a		8		8

	1
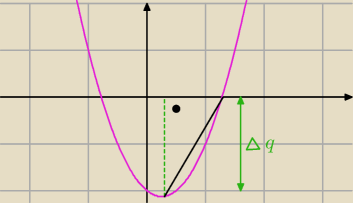
Odległość q od osi rzędnych oznaczę Δq = 2		. Potrzeba jeszcze jednej odległości, według
	8

mnie współrzędna wierzchołka p mało tu pomoże. Trzeba obliczyć jakoś odległość między x₁ a x₂ i podzielić to na pół. tylko jak?

Mariusz:

	−Δ
Nie możesz skorzystać z wzoru na q?
	4a

Mariusz: Nie rozumiem tego.

asdf: skorzystałem, ale obliczając p wtedy będzie to już korzystanie z postaci kanonicznej..troche dziwne zadanie, ale takie było.

Mariusz: A jest coś na odległość od q? Jakiś wzór zależy od 2x²?

Mariusz: *zależny

asdf: współczynnik a określa jak jest parabola i jak szybko rośnie, nie znam na wzoru na odległość q od pierwiastków. Jedynie wzialem q od osi OX..

Bogdan: a może tak:

	1		1		1		17
2x2 − x − 2 = 0 /:2 ⇒ x2 −		x − 1 = 0 ⇒ x2 − 2*x*		+		−		= 0
	2		4		16		16

	1		√17
(x −		)2 − (		)2 = 0
	4		4

	1		√17		1		√17
(x −		−		) (x −		+		) = 0
	4		4		4		4

	1 + √17		1 − √17
x =		lub x =
	4		4

asdf: Dzięki