Wyznacz równanie prostej przechodzącej przez punkt P(-3, -1) i prostopadłej do p Pawelxx: Wyznacz równanie prostej przechodzącej przez punkt P(−3, −1) i prostopadłej do prostej l. l: 3x + 5y − 1 = 0 Proszę o pomoc.

Dominik:

	1
−		x + 5y + c = 0
	3

	1
−		*(−3) + 5 * (−1) + c = 0
	3

wyznacz c i podstaw pod 1 rownanie

Janek191: P = ( − 3; − 1) l : 3 x + 5y − 1 = 0 Zapisuję równanie prostej l w postaci kierunkowej: 5y = −3 x + 1 y = (−3/5) x + 1/5 a = − 3/5 Warunek prostopadłości prostych: a*a₁ = − 1 zatem ( − 3/5)*a₁ = − 1 a₁ = 5/3 Równanie dowolnej prostej prostopadłej do danej: y = a₁ x + b₁ czyli y = ( 5/3) x + b₁ Ma ona przechodzić przez P = ( − 3; − 1) , więc − 1 = (5/3)*(−3) + b₁ − 1 = − 5 + b₁ −1 + 5 = b₁ b₁ = 4 zatem Odp. y = (5/3) x + 4 ===================== 3 y = 5x + 12 5x −3y + 12 = 0 − postać ogólna równania =========================================

Pawelxx: Po podstawieniu mam (4 to C): − 1/3x + 5y + 4 = 0 A w kluczu jest odpowiedź: y = 5/3x + 4 Co powinienem zrobić?

Pawelxx: Dzięki @Dominik i @Janek191.

Mila:

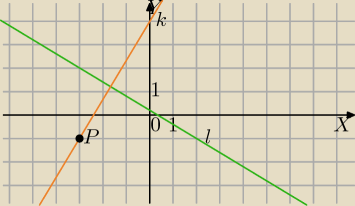
	3		1
l: 3x + 5y − 1 = 0 [5y=−3x+1;y=−		x+		]
	5		5

k: 5x−3y+C=0 prostopadła do prostej l 5*(−3)−3*(−1)+C=0 −15+3=−C −12=−C C=12

	5
k:5x−3y+12=0 [−3y=−5x−12; y=		x+4]
	3

k⊥l

Pawelxx: Dziękuję @Mila.

Mila:

NieOgarniamMatmy: Wyznacz równanie prostej przechodzącej przez punkt P = (−3,−1) i prostopadłej do prostej y = −4x − 3 Pliska bo nie umiem

www: https://matematykaszkolna.pl/strona/4520.html

NieOgarniamMatmy: Nie ogarniam...

Jolanta: zaczynamy od wzoru. y=ax+b Jezeli dwie proste są równoległe to mają takie samo a Jeśli sa prostopadle to a₁*a₂=−1 Nasza prosta jest prostopadła do prostej y=−4x−3 a₁=−4

	1
czyli a2=
	4

	1
y=		x+b. należy do niej punkt P(−3,−1). Pierwszy w nawiasie jest x,drugi y.
	4

Podstawiam

	1
−1=		*(−3)+b
	4

	3
−1=−		+b
	4

	1
−		=b
	4

	1		1
y=		x−
	4		4