wlasnosci prawdopodobienstwa Dominik:

	1		2
Oblicz P(B), jeżeli P(A∩B) = P(A−B) =		i P((A∪B)') =
	3		3

P(A∩B) = P(A−B) P(A∩B) = P(A) − P(A∩B)

	2
P(A) =
	3

	1
P(A∪B) =
	3

P(A) + P(B) − P(A∩B) = P(A∪B)

	1		2		1
P(B) =		−		+		= 0
	3		3		3

dobrze?

Maslanek: Pewnie nie

Maslanek: Z trzeciej podanej własności mamy:

	1
P(A∪B)=
	3

P(A∩B)=P(A)+P(B)−P(A∪B) P(A−B)=P(A)−P(A∪B). Dalej dasz sobie radę

Maslanek: W porządku jest Zaskakujący wynik

Maslanek: Nie jest dobrze, tylko głupota jest napisana P(A−B)=P(A)−P(A∩B)

Maslanek: Chociaż co najgorsze i tak wychodzi 0 −,−. Czyli dobrze

Dominik: P(A−B)=P(A)−P(A∩B) to jest glupota? czy co? bo troche zamotales

Dominik: podbijam, bo w koncu nie wiem czy jest zle, czy nie.

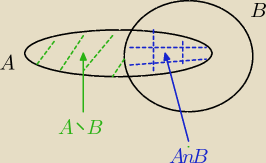
Mila: P(A\B)=P(A)−P(A∩B) tak, jakbyś liczył pole.

Artur_z_miasta_Neptuna: Dominik ... Maślanek na poczatku napisał: P(A−B)=P(A)−P(A∪B). I dlatego później napisał, ze to głupota (bo wtedy P(A−B) ≤ 0 dla dowolnych A,B∊Ω

Dominik: okej, dzieki. czyli P(B) rzeczywiscie wynosi 0.

Dominik: chociaz nie rozumiem. jesli P(B) = 0 to P(B∩A) powinno wynosic tez 0 (czesc wspolna zbioru A i zbioru pustego to raczej 0).

Artur_z_miasta_Neptuna: Bo jest błąd w zadaniu <−−− dlatego wyniki są speczne