zad
OLA: korzystając z def granicy w sensie Heinego wykaż, że nie istnieje granica:
lim (przy x→1) arctgx
proszę o pomoc!
3 sty 14:27
PW: Jak patrzę na wykres tangensa, to zastanawiam się: dlaczego funkcja odwrotna miałaby nie mieć
granicy w jedynce?
3 sty 14:46
Artur_z_miasta_Neptuna:
hmmm ... ciekawe ciekawe ... jak funkcja ciągła może nie mieć granicy w punkcie należącym do
dziedziny ... hmmm
3 sty 14:51
asdf:
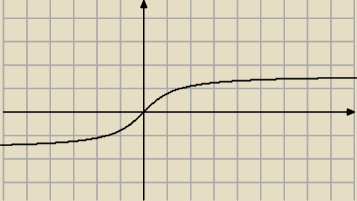
no jak nie ma granicy w x→1...?
3 sty 14:53
OLA: kurcze, nie wiem wlasnie jak to udowodnic, bo mi sie nic nie zgadza
3 sty 15:10
Artur_z_miasta_Neptuna:
to Ci piszemy −−− że nie da się udowodnić czegoś co jest nieprawdą
zapewne źle przepisałaś przykład
3 sty 15:11
Artur_z_miasta_Neptuna:
| | 1 | |
zapewne chodziło o np. arctg |
| |
| | x−1 | |
3 sty 15:11
OLA: dobrze przepisałam...
mozliwe, ze na kartce, z zadaniami ktore mam od wykladowcy są błędy
3 sty 15:14
Artur_z_miasta_Neptuna:
możliwe
3 sty 15:15
OLA: a jak z tym by było:
lim ( x→π+) 1sinx
3 sty 15:18
asdf: −∞
3 sty 15:20
Artur_z_miasta_Neptuna:
ale co masz zrobić
pokazać że granica nie istnieje
| | 1 | |
granica prawostronna wyrażenia |
| istnieje i wynosi −∞ |
| | sinx | |
3 sty 15:20
OLA: no a mam udowodnic ze nie istnieje
3 sty 15:29
Artur z miasta Neptuna:
Granica jednostronna istnieje .... ale granica (ogolnie) nie istnieje
Tak wiec sprawdz dokladnie jak wygladaja przyklady
3 sty 17:19