Wyznacz wszystkie pierwiastki liczby zespolonej Agnieszka: Wyznacz wszystkie pierwiastki ³√i−1 Wiem, że mają byc trzy rozwiązania. Może ktoś pomoże i naprowadzi?

Krzysiek: zamień liczbę z=−1+i na postać trygonometryczną i skorzystaj ze wzoru de Moivre'a

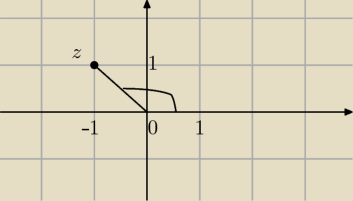
Mila: ³√−1+i z=−1+i punkt(−1;1) |z|=√2

	3π
φ=
	4

	3π   +2kπ 4		3π   +2kπ 4
zk=3√√2*(cos(		)+isin(		) dla ∊{0,1,2}
	3		3

	π		π		√2		√2
z0=6√2cos(		+isin		)=6√2(		+i		)
	4		4		2		2

licz dalej