tw talesa
Marcin17: Przekątne trapezu ABCD o podstawach AB i CD przecinają się w punkcie S.
Wiedząc że pola trójkątów ABS i CDS wynoszą odpowiednio 9 i 16
oblicz pole trapezu. Wykonaj odpowiedni rysunek.
2 sty 21:33
Marcin17: Czy ktokolwiek umie to zrobić?
2 sty 22:14
Aga1.:
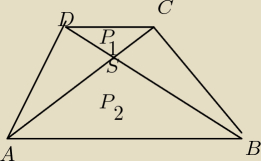
P
1=9, P
2=16
Najkrócej
P
tr=(
√P1+
√P2)
2=(3+4)
2=49
2 sty 22:17
Aga1.:
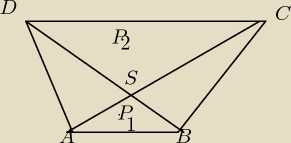
Poprawię pomocniczy rysunek
2 sty 22:23
Marcin17:
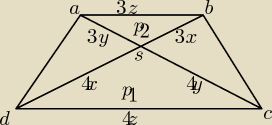
z czego wynika ten wzór? nigdy go nie widziałem?
ja zastanawiałem się raczej nad podobieństwem tzn P1/P2=k
2 więc skala podobieństwa wynosi
k=4/3
oznaczyłem DS=4x, SB=3x, CS=4y, SA=3y
wiem że pola trójkątów CSB i DSA są takie same ale nie wiem jak je obliczyć?
2 sty 22:28
Tad:
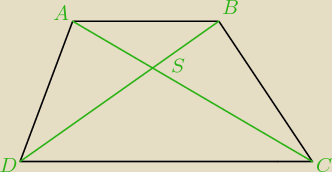
... zgodnie z treścią (choć sądzę, że przestawiłeś kolejność okreslając pola trójkątów)
Trójkąty ABS i CDS są podobne ... skalę podobieństwa k obliczysz ze stosunku pól
... a dalej to już banał −
2 sty 22:33
Marcin17: nie przestawiłem treści wszystko jest dokładnie przepisane. No właśnie tego banału nie wiem jak
rozwiazać
2 sty 22:34
Aga1.:
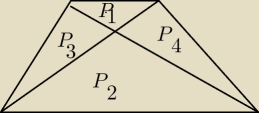
Uzasadnienie
P
tr=P
1+P
2+P
3+P
4, ale P
3=P
4
P
tr=P
1+2P
3+P
2=(
√P1+
√P2)
2
2P
3=2
√P1*P2
P
3=P
4=
√P1*P2
2 sty 22:36
Tad:
a możesz to zrobić również tak |CD|=x a wys.ΔCDS=y
| |AB|+|CD| | | x+(3/4)x | | 7x | |
| = |
| = |
|
|
| 2 | | 2 | | 8 | |
| | 7y | |
wys trapezu to y+(3/4)y= |
|
|
| | 4 | |
| | 7x | | 7y | | 49xy | | 49*32 | |
zatem pole trapezu to |
| * |
| = |
| = |
| =49
|
| | 8 | | 4 | | 32 | | 32 | |
zauważ, że xy/2=16 ⇒xy=32
2 sty 22:49
Marcin17: kurde że sam na to nie wpadłem że przecież skala podobieństwa dotyczy nie tylko boków ale też
innych odpowiednich odcinków np. wysokości
dzięki wszystko jasne
2 sty 22:57
Tad: −
2 sty 23:07
Eta:
Słabe to uzasadnienie ( a właściwie ... brak uzasadnienia
21 mar 00:12
21 mar 00:49