geometria analityczna byakuya: Dany jest punkt P(3,4) oraz wektor AB =[−1,2]. Znajdź równanie prostej k prostopadłej do wektora AB o przechodzącej przez punkt P. Przedstaw to rónanie w postaci kierunkowej.

Janek191: P = ( 3; 4) → AB = [ − 1; 2] zatem 2*( x − 3) + 2*( y − 4) = 0 2x − 6 + 2y − 8 = 0 2x + 2y − 14 = 0 − postać ogólna =========================== Po podzieleniu przez 2 otrzymamy x + y − 7 = 0 y = − x + 7 − postać kierunkowa ============================= Niech P₀ = ( x_o, y₀ ) oraz → v = [ a, b ] Równanie prostej przechodzącej przez P_o i prostopadłej do niezerowego wektora v : a*( x − x_o ) + b*( y − y_o ) = 0 =============================

Janek191: Znowu się pomyliłem : Winno być: − 1*( x − 3) + 2*( y − 4) = 0 − x + 3 + 2y − 8 = 0 − x + 2y − 5 = 0 − postać ogólna ============================= − 0,5 x + y − 2,5 = 0 y = 0,5 x + 2,5 − postać kierunkowa. ========================================

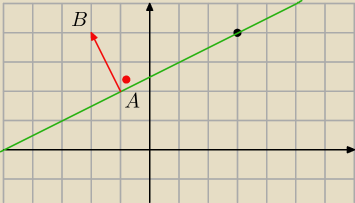
Mila: II sposób Ax+By+C=0 ogólna postać równania prostej prostopadłej do wektora [A;B] −1x+2y+C=0 P=(3;4) należy do prostej, to spełnia jej równanie. −1*3+2*4+C=0 C=−3 −x+2y−5=0 2y=x+5

	1		5
y=		x+		rownanie kierunkowe.
	2		2