pytanie
tn: P(B−A) =
Jak to rozpisać?
1 sty 21:58
Artur_z_miasta_Neptuna:
P(B\A) = P(B) − P(A∩B)
1 sty 21:59
tn: Ok, a skąd takie coś, w sensie taka rozdzielność?
BO wiem, że
P(B−A) = P( B − A∩B)
1 sty 22:07
1 sty 22:10
Mila:
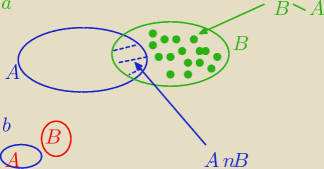
a) A∩B≠Φ
P(B\A)=P(B)−P(AnB) ( zasada jak pole figury)
b)A∩B=Φ
B\A=B
P(B\A)=P(B)
1 sty 22:18
pigor: ... no to dalej "jedziesz"
tn; ponieważ zbiory B i A∩B są
rozłączne to twoje
P(B−A)= P(B−A∩B)=
P(A)−P(A∩B) i tyle . ...
1 sty 22:20
Mila: Pigor, nie masz pomyłki?( literówka?)
1 sty 22:24
asdf: @Mila
mogłabyś zajrzeć do tych funkcji cyklometrycznych?
1 sty 22:27
Mila:
@ASDF Podrzuć do góry, bo szukałam i nie znalazłam.
1 sty 22:28
pigor: ... dzięki, przepraszam (pierwszy dzisiaj post i ...) miało być: nie A tylko
B, czyli
P(B−A)= P(B−A∩B)= P(
B)−P(A∩B) i tyle . ...
1 sty 22:34
tn: Mila, mam rozumieć, P(B\A)=P(B)−P(AnB) że zachodzi tylko wtedy gdy A i B są rozłączne?
Rzeczywiście, jak pole figury
P.S A jak rozpisać (A∩B)
1 sty 22:34
Mila:
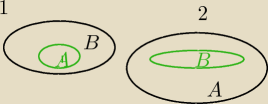
Po co chcesz rozpisać.?
Jest wzór na prawdopodobieństwo sumy zbiorów
P(A∪B)=P(A)+P(B)−P(A∩B) stąd można czasem obliczyc P(A∩B)
1) A⊂B
A∩B=A
P(A∩B)=P(A)
2)B⊂A
A∩B=B
P(A∩B)=P(B)
I co jeszcze Cię interesuje?
1 sty 22:57
tn: A co jeśli są rozłączne?
1 sty 23:05
tn: MIla, mam po prostu wykazać:
1 sty 23:06
Mila: Napisz całą treść zadania.
Zdarzenia A i B mogą być różne.(zależne, niezależne, rozłączne)
1 sty 23:13
tn: One należą do OMEGI
1 sty 23:15
tn: P(A∪B)=P(A)+P(B)−P(A∩B) ,
Czy ten wzór mogę przekształcać jak równanie?
1 sty 23:16
Mila: Możesz.
P(A')=1−P{A)
0≤P(A∪B)≤1
1 sty 23:24
Mila: | | 1 | | 9 | |
Tam masz p(A ' )≥ |
| ? czy |
| ? |
| | 10 | | 10 | |
1 sty 23:34
tn: 9/10
1 sty 23:36
tn: WIedząc To mam pokazać, że zachodzi tamto powyższe AnB < 1/5
1 sty 23:37
Mila:
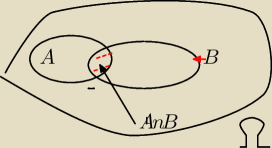
P(A∩B) może mieć największą wartość równą P(A)
| | 1 | | 1 | | 2 | |
P(A∩B)≤P(A)< |
| < |
| = |
| |
| | 10 | | 5 | | 10 | |
2 sty 00:01
tn: Mogę robić takie operacje jakby to była funkcja Pola?
2 sty 00:21