. asdf: granice funkcji: mam taki przykład: obliczyć granice ciągu w punkcie x₀ = 2

	x+2
f(x) =
	x−1

	x+2
Df =		, x ≠1, x∊ (−∞;1)(1;∞)
	x−1

a co dalej?

Aga1.: liczysz po prostu f(2)

	x+2		2+2
limx→2		=		=4.
	x−1		2−1

Artur_z_miasta_Neptuna: podstawiasz x₀ = 2 i podajesz wartość

Mateusz: za x podstawiasz 2 i koniec

asdf: Sorry, zapomniałem dodać: obustronnie, czyli x→2⁻ x→2⁺ Dla prawej właśnie tak policzyłem, dla lewej nie wiem jak

Aga1.: I dla prawostronnej i lewostronnej tak samo jak wyżej.

asdf: Nie rozumiem Na wolframie to tak widać: http://www.wolframalpha.com/input/?i=lim+%28+%28x%2B2%29%2F%28x-1%29+%29+and+x-%3E2 z lewej jakby zbiega do −∞; z prawej do 4..

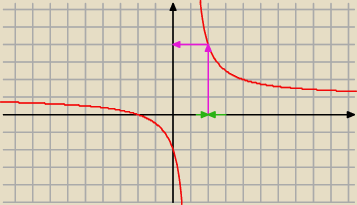
asdf: a nie. z lewej to też zbiega do 4 tak? (drugą asymptote pomijam, jest ona do wartości=1; Tylko ta prawa asymptota przecina x = 2, czyli z lewej i z prawej jest = 2

Aga1.:

asdf: a jak mam taki przykład: x₀ = 2

	x+2
x→x0
	2−x

D: R / {2}

	4		4
x→2− =		= [		]
	2−2−		0

2⁻, czyli ta wartość należy od(−∞;2), jest co raz bliżej ale jej nie przekracza, czyli podstawie sobie: 1,99999

4		4
	=		= +∞
2−1,999		0+

	4		4
dla x→2+ =		=
	2−2+		0

2⁺, czyli wartośc należy od (2;∞), jest coraz bliżej ale jej nie przekracza, czyli podstawie sobie: 2,00001

4		4
	=		= −∞
2−2,00001		0−

tak? granica w punkcie x₀ nie istnieje.

Aga1.: Nie istnieje, bo granica lewostronna nie równa się granicy prawostronnej.

asdf: a rachunki są dobrze zrobione?

Aga1.: Tak, jeśli znasz tylko taki sposób.

asdf: Wiem, że ten jest taki "na odwal się", jest jakiś porządniejszy?

Artur_z_miasta_Neptuna:

	4		4
to nie jest na odwal ... tylko staraj się nie pisać		=
	2−2,0001		0−

	x+2		4
tylko po prostu limx−>2+		= [		] = −∞
	2−x		0−

asdf: A jest jakiś sposób z x_n, gdzie x_n = ta sama granica co granica funkcji, tylko to dla granicy ciągu(n→∞) itd. Kojarzycie to?

Maslanek: x₀→2 Weźmy dwa ciągi:

	1
an=2+
	n

	1
bn=2−		.
	n

x₀→2= lim(n→∞) a_n = lim(n→∞) b_n. Podstaw te dwa ciągi zamiast x₀ (x). I wykaż, że g₁≠g₂. Trochę dupny zapis, ale już mi się zapomniało