zadanie z okręgiem Ratarcia: W okrąg wpisano czworokąt wypukły ABCD taki, że jego przekątna AC leży na średnicy okręgu, a druga przekątna BC i bok DC są takiej samej długości. Punkt P przecięcia się przekątnych czworokąta jest tak położony ,że długość odcinka AP stanowi 3/5 promienia okręgu. Zapisz długość AB w zależności od promienia okręgu.

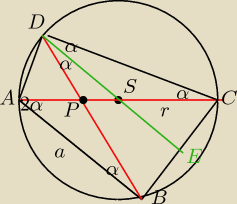
+-: AP=0,6r PS=0.4r DPC=APB=180−3α

a		AP		a		0,6r
	=		→		=
sin(180−3α)		sinα		sin(180−3α)		sinα

DS		PS		r		0,4r
	=		→		=
sin(180−3α)		sinα		sin(180−3α)		sinα

Po podzieleniu stronami otrzymujemy

a		0,6
	=
r		04

	3
AB=		SC
	2

Ratarcia: dziękuję

+-: a/r=06r/04r wynika z bezpośrednio z podobieństwa ΔDPS I ΔABP

Ratarcia: ok.