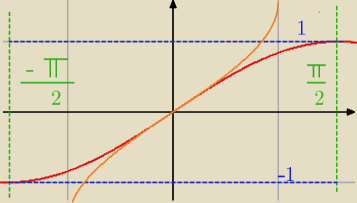
. asdf: funkcje cyklometryczne: Jak się wyznacza dziedzinę funkcji cyklometrycznych? Zgubiłem notatki i a mi bardzo potrzebne jest to na piątek (na internecie nie mogę znaleźć tego): Funkcja cyklometryczna to odwrotność funkcji trygonometrycznej: 1^o Określa się przedział gdzie funkcja jest różnowartościowa ( nie powtarza się)

	π		π
dla sinusa: x∊(−		;		)
	2		2

2^o Rysuje się dla niej wykres w tym przedziale (zaznaczając ZWF i DF)

	π		π
ZWF = <−1;1>; DF = (−		;		)
	2		2

Czyli jakby: rysunek jest ograniczony: z góry przez 1 z dołu przez −1,

	π
z prawej przez		,
	2

	π
z lewej przez −
	2

3^o Korzysta się z funkcji y=x i zamienia się x na y(zwf na df), y na x (df na zwf):

	π		π
ZWF = (U{−		;		) DF = <−1;1>
	2		2

teraz rysunek jest ograniczony:

	π
z góry przez
	2

	π
z dołu przez −
	2

z prawej przez 1 z lewej przez −1 Arcus ma wartości takie jak sinus argumenty, a argumenty takie jak sinus wartości?

Mila: Po 20 wyjaśnię.

asdf: Ok, i jakbyś mogła to: Znaleźć dziedzinę funkcji:

	x
y = arccos (		)
	x+5

dla arcusa sobie już wyznaczyłem: cosx ZWF= <1;−1> DF = (0;π) arccosx: ZWF = (0;π) DF = <−1;1> ale dalej to nie wiem

asdf: .

asdf: podrzucam

Mila:

	x
F(x)= arccos
	x+5

D: x+5≠0⇔x≠−5 ( nie wolno dzielić przez 0)

	x
−1≤		≤1
	x+5

x		x
	≥−1 i		≤1⇔
x+5		x+5

x		x
	+1≥0 i		−1≤0⇔
x+5		x+5

x+x+5		x−x−5
	≥0 i		≤0⇔
x+5		x+5

2x+5		−5
	≥0 i		≤0⇔
x+5		x+5

x≥−2,5 D=<−2,5;∞) Znajdę dobrą teorię to wyślę Linka.

asdf: Dzięki. Tylko z kąd takie wyniki: x≥2,5 i dlaczego drugie pominąłaś? (mnożyć przez x+5 można?)

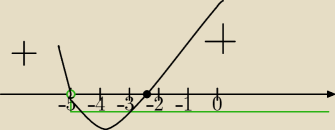
Mila: Bierzesz część współną przedziałów w których iloczyn (2x+5)*(x+5) jest dodatni i przedziału

	−5
gdzie ułamek		jest ujemny.
	x+5

Mila: http://www.zadania.info/d434/1

asdf:

2x+5
	≥ 0 // * (x+ 5)2
x+5

(2x+ 5)(x+5) ≥ 0

	5
2(x +		)(x+5) ≥ 0
	2

	5
x∊ (−∞;−5)u(−		;∞)
	2

−5
	≤ 0 // * (x+5)2
x+5

	1
−5(x+5) ≤ 0 // * −(		)
	5

x + 5 ≥ 0 x ≥ −5 część wspólna to <−2,5;∞) O to chodzi?

Mila: Tak.Masz to na ilustracji.

asdf: Dzięki

asdf: sinus też jest między −1 i 1?

asdf: arcsin*

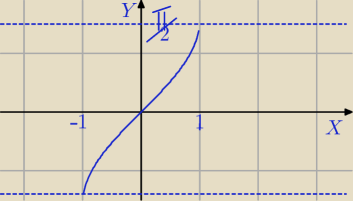
Mila: y=arcsin(x) D: x∊<−1;1>

	−π		π
ZW: y∊(		;		)
	2		2

ale to są głowne przedziały wartości, na studiach chyba obowiązują wszystkie przedziały , co Wam mówili?

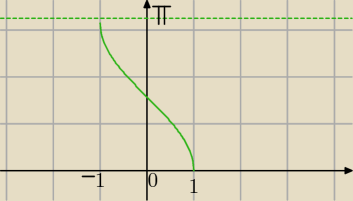
Mila: y=arccos(x) D=<−1;1> ZW=<0;π>

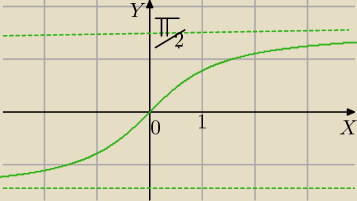
Mila: y=arctg(x) x∊(−∞;∞) dziedzina

	π		π
y∊(−		;		)
	2		2

asdf: Wykładowca nam pierw wyjaśnił czym jest funkcja, pozniej czy jest funkcja odwrotna (ze funkcja jak nie jest roznowartosciowa to nei ma funkcji odwrotnej), pozniej skrocila, zeby byla roznowartosciowa i narysowala do tego funkcje odwrotna. powiedziala ze odwrotna do tryg. to cyklometryczna. Nie mam dokladnych notatek

Mila: To zrób te zadania co Ci wskazałam i poszukaj na forum innych, było sporo.

asdf: Ok, dzięki.

Mila: dobranoc

asdf: Dobranoc