Równania kwadratowe
Paulina: Drut długości 64 cm podzielono na dwie części. Z jednej części wykonano kwadratową ramkę, a z
drugiej ramkę prostokątną w której stosunek długości boków wynosi 3:1. Suma powierzchni
ograniczonych prze obie ramki wynosi 112 cm
2. Na części jakiej długości został podzielony
drut.
Mam coś takiego
4x+2(y+3y)=64
x
2+3y*y=112
4x+8y=64
x+2y=16
x=16−2y
(16−2y)
2+3y
2=112
256−64y+4y
2+3y
2−112=0
7y
2−64y+144=0
Δ = 4096−4*7*144=64
√Δ=8
y
1=4
I tutaj stanęło zadanie. Co dalej. Pomóżcie, naprowadźcie na właściwy trop. HELP


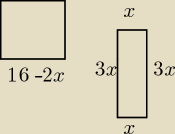 Jedna część 8x, druga 64−8x
(16−2x)2+3x2=112
x>0 i 16−2x>0
Jedna część 8x, druga 64−8x
(16−2x)2+3x2=112
x>0 i 16−2x>0
