podprzestrzen opis
gakusei: Opisz podprzestrzen V
1⊂V=R
3
V
1=lin[v
1,v
2] v
1=(1,0,0) v
2=(0,0,1)
Jak sie za to zabrac?
1 sty 13:47
Trivial:
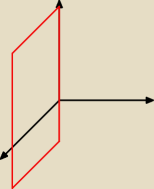
Wszystkie punkty w tej przestrzeni spełniają równanie:
P = x*(1,0,0) + z*(0,0,1) = (x, 0, z). Dla dowolnych x,z.
Zatem jest to płaszczyzna xOz.
1 sty 14:00
gakusei: nie do końca rozumiem rysunek
w sensie ten wektor po skosie to jest v
2, a v
1 to ten do
gory?
1 sty 14:59
1 sty 17:46
gakusei: jakos nie moge przelozyc tych rownan na to ktore zapisales
, moglbys je objasnic? wybacz, ze
tak trudze, ale przestrzenie nie sa moja mocna strona
2 sty 12:56
Trivial:
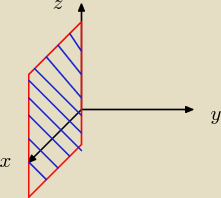
lin(v
1, v
2) − podprzestrzeń, którą opisuje kombinacja liniowa wektorów v
1,v
2
Liniowa kombinacja tych wektorów to: c
1*v
1 + c
2v
2, gdzie c
1,c
2 są dowolnymi stałymi.
Zatem wszystkie punkty tej podprzestrzeni spełniają równanie:
P = c
1*v
1 + c
2v
2 = c
1*(1,0,0) + c
2*(0,0,1) = (c
1,0,0) + (0,0,c
2) = (c
1, 0, c
2)
Czyli wystarczy aby punkt P miał zerową współrzędną y (dowolny x, dowolny z). Wtedy należy do
lin(v
1,v
2). Takie punkty zawiera płaszczyzna xOz.
Nie wiem jak to prościej wyjaśnić.
2 sty 13:31
gakusei: swietny opis, dziekuje!
2 sty 15:08