Geometria Tomek: Hej przy przygotowaniu do olimpiady pojawiły się trudności z tym zadaniem. Mógłby ktoś pomóc? Bok BC trójkąta ABC ma długość 12. Poprowadzono środkową DB boku AC. Znajdź długości odcinków na które bok BC jest podzielony prostą przechodzącą przez wierzchołek A i środek środkowej BD. (wykonaj rysunek pomocniczy)

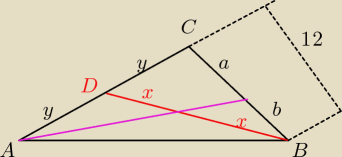
Maslanek: To ja zrobiłem rysunek

Maslanek: Pewnie to zły trop, ale:

	y		2x
z twierdzenia sinusów mamy (ΔBCD):		=
	sin <CBD		sin <DCB

	y		2x
podobnie (ΔABD):		=		.
	sin <ABD		sin <BAD

Czy z tego wynika, że odpowiednie kąty są równe?

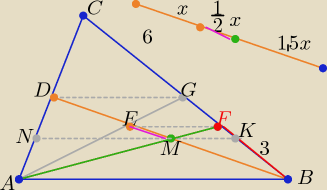
Eta: Teraz już z górki , rozpatrzeć odpowiednie trapezy i ich własności , napisać ładny komentarz oraz skorzystać z rady poczciwego Talesa i otrzymujemy: |BF|= 4 , |FC|= 8

Eta: A swoją drogą ... bardzo fajne zadanie

Maslanek: Ta spoko xD Ciekawe

Eta: Maślanek i co się tak cieszysz ?

Maslanek: Z Twojej wyższości