funkcja nn2cc: f(x)=x⁴−4x³+4x²−117 wyznacz maksymalne przedzialy w ktorych funkcja jest rosnaca Czy można narysować funkcję g(x)=x⁴−4x³+4x² jej miejsca zerowe to 0 i 2, rysuje wykres wielomianu, , ich srednia to 1 , czyli rosnie od <0,1> i <2,+∞) ?

Aga1.: Raczej obliczasz pochodną i tam gdzie pochodna jest dodatnia tam dana funkcja jest rosnąca f⁽x)=4x³−12x+8x

nn2cc: wlasnie nie umiem pochodnych, a chcialem sie dowiedziec czy moj sposob jest ok

Maslanek: Dla funkcji kwadratowej tak (prawie na pewno ). Dla innych nie.

Maslanek: Dla funkcji kwadratowej na pewno...

nn2cc: no ale tutaj mam dwa pierwiastki tyle ze podwójne, wiec tez to działa. Chyba zawszze jak sa dwa

	x1+x2
miejsca zerowe i n−krotne pierwiastki, to mozna obliczyc ich srodek z
	2

nn2cc: byleby te miejsca zerowe byly tego samego stopnia

Aga1.: f↗ w przedziale(−1,0) f↗ (1,∞) Można rysować wykres f(x) i odczytać z wykresu przedziały monotoniczności

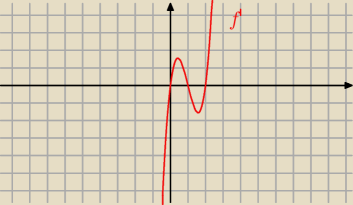
Aga1.: Przepraszam, źle zapisałam pochodną f^'(x)=4x³−12x²+8x f↗ (0,1) f↗(2,∞)

nn2cc: czyli ze sie zgadza, a przedialy nie powinny być <> ? przeciez maksymalne trzeba

Aga1.: Jak maksymalne( nie doczytałam), to trzeba domknięte.