Różnica w przekształceniach wykresów funkcji trygonometrycznych Cusack: Nie rozumiem jaka jest różnica pomiędzy wykresami tych funkcji: 1) f(x)=sin(|x|+^π₃) 2) f(x)=sin(|x+^π₃|) Drugi przykład rozumiem w ten sposób, że sin|x| przesuwam o wektor [−^π₃,0], ale w takim razie jak interpretować pierwszy?

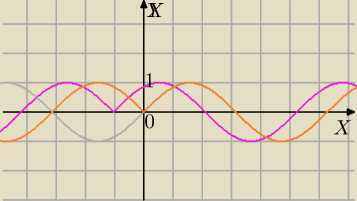
Mila: zadanie 2) 1) y=sinx popielaty 2)odbicie względem OY⇒ y=sin|x| pomarańczowy

	π		π
3)translacja o wektor[−		;0] ⇒ y=sin(|x+		|)
	3		3

Cusack: Dzięki Mila, czyli dobrze myślałem co do drugiego. Ale jak pierwszy?

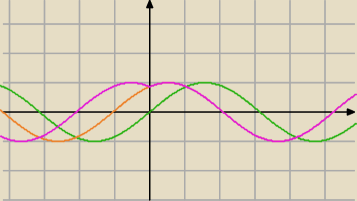
Mila: 1) sin(x)

	π		π
2)translacja o wektor [−		;0]⇒y=sin(x+		) pomarańczowy
	3		3

	π
3) symetria względem OX prawej strony wykresu ⇒y=sin(|x|+		) różowy
	3

PW: Dla x<0 jest to sin(−x+^π₃), a dla x≥0 jest to sin(x+^π₃)

Cusack: ok, dzięki.

Mila: A najlepiej to rozpisać, gdy się myli .( zobacz PW)