dwa zadania tn: Witam. 1. W pierwszej urnie jest 6 kul czarnych i 4 białe, a w drugiej urnie 7 czarnych i 8 białych. Losujemy dwie kule bez zwracania z pierwszej urny i dwie kule ze zwracaniem z drugiej urny. Jakie jest prawdopodobieństwo wylosowania dokładnie trzech kul białych Tego zadania nie rozumiem w ogóle. 2. W sklepie owocowo−warzywnym w sprzedaży jest sześć odmian jabłek. Każdy z sześciu klientów, którzy dokonali zakupów w tym sklepie w ciągu ostatniej godziny, kupił kilogram jabłek. Oblicz prawdopodobieństwo zdarzenia: B−trzy osoby kupiły jabłka tej samej odmiany, a pozostałe trzy kupiły jabłka różnych odmian. Tutaj w tym drugim, Nie rozumiem. Niby otrzymałem wynik jaki trzeba, ale jednak nie wiem dlaczego dobrze. Popatrzcie: Wybieram trójkę osób. Kombinacja 3 z 6. Mnożę razy sześć, bo na tyle sposobów ta trójka może wybierać sobie jeden rodzaj. Potem powinienem mnożyć razy 5 * 4 * 3. Ale wg mnie, powinienem potem mnożyć razy: (3*5) * (2*4) * (1*3). Dlatego tak, ze potrzebuję, że wybieram najpierw osobę, a potem dla niej jakąś odmianę. Dlaczego więc nie powinno być tak jak ja napisałem?

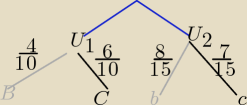
Eta: Z U₁ −− losowanie bez zwracania , z U₂ −−− losowanie ze zwracaniem zd.A={ (B,B, b, c) (B,C,b, b)}

	4		3		8		7		4		6		8		8
P(A)=		*		*		*		+		*		*		*		=.....
	10		9		15		15		10		9		15		15

PW: Strasznie podchodzisz do rozwiązywania zadań. Jest to sposób, który skrótowo określam nazwą "Jak to się robi", odpowiedź brzmi − "to trzeba pomnożyć". Elementarz: skonstruuj przestrzeń zdarzeń elementarnych Ω (inaczej mówiąc opisz wszystkie możliwe zdarzenia, nic jeszcze nie licząc). No więc: zdarzeniami elementarnymi są wszystkie możliwe przyporządkowania "klient → odmiana jabłka". Klienci są w sposób naturalny uporządkowani przez kolejność przychodzenia do sklepu. Dobrym modelem matematycznym będą więc wszystkie ciągi sześciowyrazowe o wartościach w zbiorze {1,2,3,4,5,6}. Na przykład jednym ze zdarzeń jest (3,4,1,1,2,6) − ciąg ten ilustruje przypadek "pierwszy klient nabył jabłka trzeciej odmiany, drugi klient − jabłka czwartej odmiany, trzeci i czwarty klient kupili jabłka pierwszej odmiany, piąty − drugiej i szósty − szóstej. takie ciągi nazywane są 6−elementowymi wariacjami z powtórzeniami o wartościach w zbiorze 6−elementowym. Oczywiście tego wszystkiego w rozwiązaniu zadania nie musisz pisać − wystarczy Ω = {(a₁,a₂,a₃,a₄,a₅,a₆): a_i∊{1,2,3,4,5,6}}, |Ω| = 6⁶ Jeżeli jednak tego nie zrobisz, tylko zaczynasz gorączkowo kombinować − co przez co pomnożyć, żeby "wyszło", to przepadłeś. Spróbuj teraz elegancko opisać: jakie wariacje tworzą zdarzenie B.

tn: Dzięki Wam za wsparcie! Jutro przeanalizuję co napisaliście na spokojnie Dzięki wielkie za zaangażowanie

Mila: zadanie 2)

6 3
	wybrana trójka osób (kupi tę samą odmianę)

6 1
	wybór odmiany

V₅³=5*4*3 to 3 wyrazowe wariacje bez powtórzeń z 5 elementów

	6 3
|B|=		*6*5*4*3

Eta:

Mila: 1) mamy sytuacje sprzyjające:

	4 2
BBBC		*8*7=6*56

	4 2
BBCB		*7*8=6*56

	4 1		6 1
BCBB		*		*82=24*64

z I urny kolejność nie jest ważna w drugiej tak Czarnym kolorem I urna czerwony II urna

	6		56		24		64
P(A)=2*		*		+		*		=
	10 2		152		10 2		152

	736
=
	153

Eta: Echh .... zapomniałam o kolejności

Mila: Witaj Eto, nie sprawdzałam Twojego rozwiązania, ale pamiętam, że moi uczniowie zawsze mają problem z tym zadaniem.

Eta: Na to samo wyjdzie i moim sposobem po dorzuceniu jeszcze (BBcb)