awdawd
bolo: dany jest ostrosłup prawidłowy czworokątny. krawędz podstawy ostrosłupa ma długość 6 a kąt
między sąsiednimi ścianami bocznymi. Moze mi ktos to narysowac ? Mysle ze z policzeniem nie
bedzie problemu
29 gru 19:53
Tad:
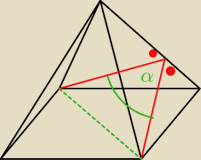
29 gru 20:23
bolo: jednak z policzeniem tez sa problemy... wiem ze moge policzyc dl ( u ciebie czerwonych linii

) z tw cosinusow, a przekatna to 6
√3. Tutaj staje.
30 gru 12:01
Aga1.:
Nie napisałeś co masz obliczyć i ile wynosi α.
przekątna (zielona) d=a√2=6√2
d2=h2+h2−2h2cosα, gdzie h − wysokość ściany bocznej, (kolor czerwony)
30 gru 12:07
bolo: zapomnialem, α=120 a mam obliczyc dlugosc krawedzi bocznej.
Licze czerwony i wychodzi mi 2√6. Potem chce podstawic do pitagorasa ( polowa podstawy, moja
czerwona i krawedz boczna) ale wynik jest zly.
Doymsalem sie, ze linia czerwona jest rowna wysokosci sciany bocznej ?
30 gru 12:22
Aga1.: Wysokość ściany bocznej ok.
30 gru 12:25
Aga1.:
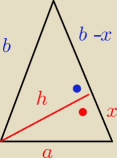
Dwa razy tw. Pitagorasa
x
2=a
2−h
2
b
2=h
2+(b−x)
2
30 gru 12:28
bolo: dzieki, rozumiem twoj sposob, a moglby mi ktos wytlumaczyc sposob z odpowiedzi ?
abcd=podstawa
s=wierzchołek ostrosłupa
BE wysokosc trojkatac BCS, BE=ED=x
SF wysokośc trójkąca BCS, SF=h −> nie rozumiem, potrzebny tez rysunek
BS=b
bed=120 stopni
wyznaczeie długości wysokości ściany bocznej x=2√6, to mam (czy mozna tez obliczyc to z
trójkąt 90,60,30, bo 120 stopni dzieli się na połowe i tworzy trójkąt z połową przekątnej
podstawy)
uzależnienie wysokości h od długości krawędzi podstawy h=√b2−9 skąd ta "9" ?
Zapisanie równania
1/2 * b * 2√6 = 1/2 * 6 * √b2−9
2 sty 09:56
Aga1.:
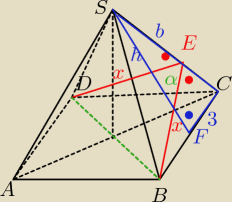
Z tego
(1)
Punkt F dzieli odcinek IBCI=6 na połowę.
W niebieskim trójkącie z tw. Pitagorasa
h
2+3
2=b
2
wylicz h i podstaw do (1)
2 sty 10:15
bolo: x nie jest jednak wysokoscia trójkąta BCS? bo wtedy była by równa h −> a=b, a tak nie jest
2 sty 10:34
bolo: podbijam
2 sty 11:30
Tad:
oczywiście, że x jest wysokością ΔBCS ... i niejest równa h bo ściana boczna jest
trójkątem równoramiennym a nie równobocznym
2 sty 11:39

 ) z tw cosinusow, a przekatna to 6√3. Tutaj staje.
) z tw cosinusow, a przekatna to 6√3. Tutaj staje.
 Dwa razy tw. Pitagorasa
x2=a2−h2
b2=h2+(b−x)2
Dwa razy tw. Pitagorasa
x2=a2−h2
b2=h2+(b−x)2
