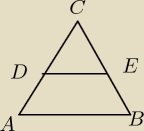
Trójkąt i srodki bokow name: Witam, otóż mam napisać dowodzenie odnośnie trójkąta , a mianowicie: Jeśli w trójkącie

	1
połączymy środki 2 boków to AB ∥DE i DE=		AB. Czy taki dowód byłby ok?
	2

Jeśli

CD		1
	=
AC		2

CE		1
	=
BC		2

to

CD		CE
	=
AC		BC

A nawiązując do twierdzenia ze jesli ramiona przetniemy dwoma prostymi, a stosunek odcinków na tych ramionach będzie taki sam to: DE∥AB A teraz twierdzenie Talesa

DE		CE		1
	=		=
AB		BC		2

	1
to DE=		AB
	2

Nie wiem czy to dobrze, bo w matmie trzeba same dowody. Trochę z książki przepisane i jak ktoś by mógł to w jakiś sposób by mi wytłumaczył bo trochę się przy tym gubię.

Artur_z_miasta_Neptuna: ja bym proponował pójść innym tropem ... mianowicie wykorzystać twierdzenie cosinusow do

	1
pokazania, że DE =		AB
	2

wtedy z podobieństwa trojkątów (kąt,bok,bok,bok) wykazujesz, że oba trójkąty (mały i duży) mają takie same kąty ... z czego dochodzisz do || podstaw

Artur_z_miasta_Neptuna: ale oczywiście Twoj dowód także jest poprawny

name: Cosinusow to jeszcze nie mam wiec nie bd mieszal Dzieki

Saizou : można też wektorami