POMOCY!!! ;/ Maciek: Dla jakich wartości parametru m równanie |x² −2mx| = 1 ma trzy różne pierwiastki?

Artur_z_miasta_Neptuna: |x²−2mx| = |x(x−2m)| = 1 i rozwiązujesz to dalej .. albo stara niezawodna metoda 'zgaduj zgaduli'

Maciek: ale jak rozwiązać to dalej?kiedy to ma 3 pierwiastki ...... to co napisałeś to już miałem

Eta: x²−2mx=1 v x²−2mx=−1 x²−2mx−1=0 v x²−2mx+1=0 Δ=4m²+4>0 ⇒m€R Δ= 4m²−4 = 4(m−1)(m+1)=0 ⇒ m=1 v m=−1 zawsze dwa rozwiązania 1 rozwiązanie Odp: trzy rozwiązania dla m..........

Maciek: dla m = 1 lub m = −1 ?

Eta:

Maciek: dziękuje slicznie, Eta pomożesz jeszcze w 1? Narysuj zbiór wszystkich punktów (x,y) płaszczyzny których współrzędne spełniają równanie log_x (y−2x) =2. Dochodze do momentu równania x(x+2)=y. Wypisuję punkty, uwzględnia że x>1, x≠0 i y> 2x. Co dalej?

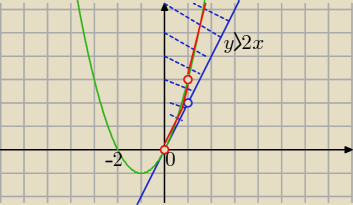
Eta: x>0 i x≠1 i y>2x i y=x²+2x=x(x+2) −−− część tej paraboli

Kam: *Do pierwszego zadania. Musisz tam jeszcze wykazać, że są to 3 różne pierwiastki. Z równania x²−2mx+1=0 dla m=1, x=1, natomiast dla m=−1, x=−1 i teraz sprawdzamy dla równania x²−2mx−1=0 czy dla m=1 wychodzi x=1∨ x=−1 lub dla m=−1, x=−1∨ x=1 jeżeli nie to w takim razie dla m∊{−1,1} wychodzą trzy różne pierwiastki.

ziom: co nieogarniam

albin55: oblicz P(A) wiedząc że P(AB) = 0,61 a P(AB")= )<0,16