pigor: ... np. tak : niech a,b,2c, c − długości boków dowolnego Δ i c − środkowej boku 2c
odpowiednio i (a,b) − kąt miedzy bokami a,b (przeciwległy bokowi 2c), to z wzoru na długość
środkowej boku 2c i tw. cosinusów względem tego boku :
c
2=
14 (2a
2+2b
2−4c
2) /*4 i 4c
2= a
2+b
2−2ab cos(a,b) ⇔
⇔ 4c
2= 2a
2+2b
2−4c
2 i 4c
2= a
2+b
2−2ab cos(a,b) ⇔
⇔ 8c
2= 2(a
2+b
2) /:2 i 4c
2=a
2+b
2−2ab cos(a,b) ⇔
⇔ 4c
2=a
2+b
2 i 4c
2= 4c
2 −2ab cos(a,b) ⇒ 0= −2abcos(a,b) ⇔
⇔ cos(a,b)=0 ⇒
(a,b)=90o c.n.w. . ...
Eta:
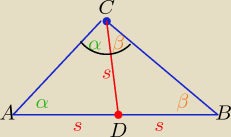
Trójkąty ADC i DBC są równoramienne o ramionach "s"
to: 2α+2β= 180
o /:2
α+β= 90
o = |∡ACB|
Trójkąt ABC jest prostokątny
c.n.u