.. asdf: Jak zbadać monotoniczność ciągu: ⁿ√5ⁿ + 6ⁿ

	5		5
n√6n(1+(		)n = 6n√1+(		)n
	6		6

i teraz: (po lewej a_n, po prawej a_n+1

5		5
	n > (		)n+1
6		6

	5		5
1 + (		)n > 1 + (		)n+1
	6		6

a^1/n > a^1/n+1 (pierwiastek ntego stopnia jest wiekszy od pierwiastka n+1 stopnia), np: −−−−−−−−−−−−−−−−−−−− 4^1/2 > 4^1/3 2 > ³√4 −−−−−−−−−−−−−−−−−−−−

	5		5
(1+(		)n)1/n > (1+(		)n+1)1/n+1
	6		6

wychodzi mi ciąg malejący...pewnie coś źle z udowodnieniem

PW: Spróbuj badać iloraz zamiast różnicy (pokazać, że iloraz dwóch kolejnych wyrazów ciągu jest większy (mniejszy) od 1 − dla ciągu o wyrazach dodatnich

	ak+1
ak+1 > ak ⇔		> 1.
	ak

asdf: czy takie coś:

	5
(1+ (		)n )n =
	6

	1		1
(1 +		)n = (1 +		)(6/5)n ]{n/(6/5)n} =
	6   ( )n   5		6   ( )n   5

e⁰ = 1? Jest to poprawne?

asdf: Nie wiem czy dobrze to zrobiłem..bo wynik to jedno, a obliczenia to drugie: http://www.wolframalpha.com/input/?i=%285%5En+%2B+6%5En%29%5E%281%2Fn%29

asdf: Chociaż to mało wiarygodne

asdf: Na necie znalazłem rozwiązanie:

	5
an = n√5n+6n = 6n√(		)n + 1
	6

Zauważmy, że dla n∊ N zachodzi nierówność:

	5		5
(		)n +1 > (		)n + 1
	6		6

Aby uzasadnić monotoniczność ciągu skorzystamy z oczywistej nierówności aⁿ > aⁿ⁺¹

	5		5		5
an+1=6*(1+(		)n+1)1/n+1<6*(1+(		)n+1)1/n<6*(1+(		)n)1/n=an
	6		6		6

Czyli miałem dobrze

asdf: tam powinno być: Zauważmy, że dla n∊ N zachodzi nierówność:

	5		5
(		)n + 1 > (		)n+1 + 1
	6		6

Artur z miasta Neptuna: Asdf ... na logike ... a1=11 ... lim an =6 oraz an>6 wiec ciag ten przynajmniej od jakiego n0 bedzie malejacy

asdf: Dzięki Idzie się bardzo dużo nauczyć dzięki tej stronie Szczególnie jak jest się mało kumatym.. mam taki przykład:

	2n+1
an =
	3n−2

	2
a1 =		= 2
	1

	5
a2 =
	4

	9
a3 =
	7

	201
a100=
	298

	10001
a5000 =		~0,6668...
	14998

	2n+3
an+1 =
	3n+1

	−7
an+1 − an =		< 0, czyli ciąg jest malejący
	9n2 + 3n − 2

Ograniczony z dołu m=0, a z góry M=2 tak?

Trivial: Artur, a skąd wiesz że nie ma oscylacji?

Artur z miasta Neptuna: No i slicznie ... oczywoscie podstawienie wyrazow Ci tylko wskazuje jakiego wyniku powinienes sie spodzoewac ... bo moze sie trafic takze ciag niemonotoniczny

Artur z miasta Neptuna: Trivial ... skoro an>6 dla kazdego n (laywo to udowodnic) a lim an=6 to istnieje taki no ze ciag ten bedzie malejacy (inaczej by nieistniala granica )

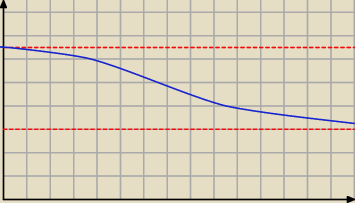
Trivial: A co jeśli wygląda tak? (:

Trivial: OK, kompromituję się. asdf, zawsze możesz podzielić wielomiany. Wtedy od razu widać.

	2n+1		2	3   3n+ −2+2   2		2		k
an =		=			=		+		, gdzie
	3n−2		3	3n−2		3		3n−2

k>0 i już stąd widać, że ciąg malejący.

asdf: Trivial, nie bardzo jeszcze rozumiem te rozwiązanie sprawdzić monotoniczność ciągu:

	2n n!
an =
	nn

	2*2n*(n+1)n!
an+1 =
	(n+1) *(n+1)n

an+1		2*2n*(n+1)n!
	=		*U {nn}{2n * n!} =
an		(n+1) *(n+1)n

2*2n*(n+1)n!		nn		2*nn
	*		=		=
(n+1) *(n+1)n		2n * n!		(n+1)n

i tu nie wiem czy można korzystać z eulera, można?

	nn		(n+1)		1		2
2 *		= 2 * (		)−n = 2 * (1+		)−n = 2 * e−1 =
	(n+1)n		n		n		e

e > 2, ciąg malejący.

asdf: a liczba k jest stałą (tylko n rośnie)

Trivial: Tak, k jest pewną stałą dodatnią (obojętnie jaką). Można ją wyliczyć ale są ułamki więc nie ma co się męczyć.

asdf: Rozwiązanie rozumiem, ale na taki sposób rozwiązania bym nie wpadł.

Mila: Do postu z 28XII z godziny 0:50

	n
2*(		)n<1 dla n>1 i to wystarczy
	n+1

Mila:

2x+1		2
	funkcja homograficzna dla x∊R\{		} i należy ją przedstawić w postaci
3x−2		3

kanonicznej (Trivial)

	1		2n+1
an=		*		=
	3		n−2/3

	1		2(n−2/3)+4/3+1
=		*		=
	3		n−2/3

	1		1   2   3		2		1   2   3
=		*(2+		)=		+
	3		n−2/3		3		3n−2

asdf:

	n
2*(		)n < 1, dla n >1 (bo według granicy "od pewnego" n coś jest w pasku epsilonowym −
	n+1

tak samo tutaj, nie musi to być od razu dla n = 1 tak?)

	n
2* (		)n.
	n+1

lim_cn = c ilm_dn = d lim_an = lim c_n * lim d_n = c* d (c jako stała = 2), czyli lim a_n = d = 0 tak?

Mila: A po co liczysz tę granicę? Miałeś (tak mi się zdaje) odpowiedzieć czy ciąg jest monotoniczny. I tu wystarczy warunek: Iloraz<1 począwszy od n>1

	n		2
lim (2*(		)n)=
	n+1		e

asdf: Dzięki