z
Midgard: Wiadomo, że do wykresu funkcji f(x) = ax2 + bx + c, a ≠ 0 należą punkty
A=(0, 2), B=(4, 2) i funkcja ta przyjmuje wszystkie wartości nieujemne.
Wyznacz wzór tej funkcji.
I tu mam pytanie, skoro pisze " funkcja ta przyjmuje wszystkie wartości nieujemne", to chodzi o
to, że ramiona idą w górę i środek ma współrzędne(2,0) ? Wzór wyszedł mi: f(x)=1/6x2−4/6
27 gru 23:02
edi:
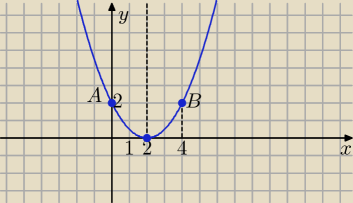
27 gru 23:15
Janek 191:
A = ( 0; 2), B = ( 4; 2)
f(x) = a x2 + b x + c , a ≠ 0
ZW = < 0; + ∞ )
zatem q = 0
f(x) = a *( x − p)2 + q = a*( x − p)2 + 0 = a*(x − p)2
oraz f(0) = 2 i f( 4) = 2
czyli
a*( 0 − p)2 = 2 i a*( 4 − p)2 = 2
a p2 = 2
a* ( 16 − 8p + p2) = 2
więc
a p2 = a*( 16 − 8p + p2) / : a
p2 = 16 − 8p + p2
8p = 16
p = 2
czyli
f(x) = a *( x − 2)2
f(4) = a*( 4 − 2)2 = 2
4 a = 2
a = 1/2
Mamy więc
f(x) = 0,5 *( x − 2)2 lub f(x) = 0,5 x2 −2 x + 2
==========================================
27 gru 23:22
