kw Midgard: Długości boków trójkąta prostokątnego są kolejnymi liczbami parzystymi, a jego pole jest równe 112 cm2. Oblicz długości jego boków. Wyszły mi takie dziwne: ^−1+√113₂, ^−1+√113₂+2, ^−1+√113₂+4

Aga1.: Przecież to nie są liczby parzyste

Midgard: więc, nie mam pojęcia jak to zrobić

Bogdan: Sprawdź Midgard zapisaną tutaj przez siebie treść zadania, słowo po słowie. Jesteś pewien, że wszystko poprawnie tu podałeś?

Midgard: Jestem pewien! kopiowałem te zadania, dostałem je od pani od matmy na maila...

Dominik: 2k − 2, 2k, 2k + 2

(2k − 2)2k
	= 112
2

pigor: ... np. tak: niech 2a, 2(a+1), 2(a+2)= ? − szukane boki Δ prostokątnego, to P_Δ=112 ⇔ ¹₂*2a*2(a+1)= 112 /:2 ⇔ a(a+1)= 56 ⇔ a(a+1)= 7*8 ⇒ a= 7, zatem 2a= 2*7= 14 cm, 2(a+1)= 2*8=16 cm, 2(a+2)= 2*9=18 cm . ...

Dominik: 14, 16, 18

Midgard: kurcze, tak też robiłem, tlyko tyle, że zapomniałem, że przy polu trójkąta dzieli się na 2... eh... Dzięki!

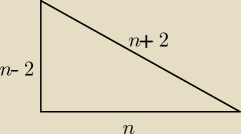
Bogdan: No to przetestujmy twoją pewność. Rysunek przedstawia trójkąt prostokątny, którego długości boków są kolejnymi liczbami parzystymi: n−2, n, n+2. Zastosuj twierdzenie Pitagorasa i oblicz wartość n.

Bogdan: Trójkąt o bokach 14, 16, 18 nie jest prostokątny, a więc nie są spełnione warunki zadania.

Aga1.: Ale 14²+16²=452 a 18²=324

Midgard: No proszę. Aż chyba zapytam się pani.